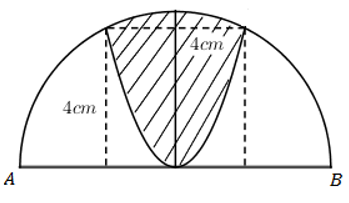
Cho nửa đường tròn đường kính \(AB=4\sqrt{5}\). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hia điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
Phương pháp giải
Ứng dụng tích phân để tính thể tích khối tròn xoay.
Lời giải của Tự Học 365
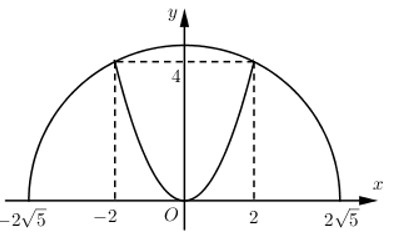
Gắn hệ trục tọa độ Oxy như hình vẽ:
Ta có:
Phương trình đường tròn: \({{x}^{2}}+{{y}^{2}}=20\Rightarrow y=\sqrt{20-{{x}^{2}}}\)
Phương trình parabol: \(y={{x}^{2}}\)
Thể tích khối cầu \(V=\frac{4}{3}\pi {{\left( 2\sqrt{5} \right)}^{3}}=\frac{160\sqrt{5}}{3}\pi \)
Thể tích khi quay phần tô đậm quanh trục $Ox$ là: \(V'=\pi \int\limits_{-2}^{2}{\left( 20-{{x}^{2}}-{{x}^{4}} \right)dx}=\frac{928}{15}\pi \)
\(\Rightarrow \) Thể tích cần tính \({{V}_{1}}=V-V'=\frac{160\sqrt{5}}{3}\pi -\frac{928}{15}\pi =\frac{\pi }{15}\left( 800\sqrt{5}-928 \right)\)
Đáp án cần chọn là: b
Toán Lớp 12
