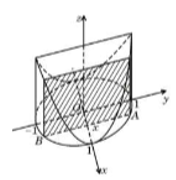
Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình \({x^2} + {y^2} = 1\) và mỗi thiết diện vuông góc với trục \(Ox\) là một hình vuông (tham khảo hình vẽ bên).
Phương pháp giải
Sử dụng công thức tính thể tích phần vật thể giới hạn bởi hai mặt phẳng \(x = a,x = b\) là \(V = \int\limits_a^b {S\left( x \right)dx} \), ở đó \(S\left( x \right)\) là diện tích thiết diện khi cắt vật thể bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\left( {a \le x \le b} \right)\).
Lời giải của Tự Học 365
Quan sát hình vẽ, ta thấy thiết diện là hình vuông cạnh \(AB\).
Gọi \(H = AB \cap Ox \Rightarrow OH = x,OA = 1 \Rightarrow AH = \sqrt {1 - {x^2}} \) \( \Rightarrow AB = 2\sqrt {1 - {x^2}} \Rightarrow S\left( x \right) = A{B^2} = 4\left( {1 - {x^2}} \right)\).
Vật thể đã cho giới hạn bởi hai mặt phẳng \(x = - 1,x = 1\) và có diện tích thiết diện \(S\left( x \right) = 4\left( {1 - {x^2}} \right)\) nên có thể tích \(V = \int\limits_{ - 1}^1 {4\left( {1 - {x^2}} \right)dx} = \left. {\left( {4x - \dfrac{4}{3}{x^3}} \right)} \right|_{ - 1}^1 = \dfrac{{16}}{3}\).
Đáp án cần chọn là: a
Toán Lớp 12
