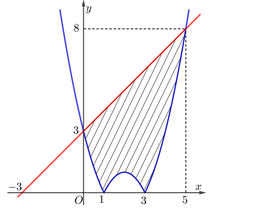
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y=\left| {{x}^{2}}-4x+3 \right|,\,\,y=x+3\) (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) bằng
Phương pháp giải
Bản chất bài toán là tính tích phân của hàm chứa trị tuyệt đối
Lời giải của Tự Học 365
Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm phương trình \(\left| {{x}^{2}}-4x+3 \right|=x+3\Leftrightarrow \left[ \begin{align} x=0 \\ x=5 \\ \end{align} \right..\)
Khi đó, diện tích của \(\left( H \right)\) là \(S=\int\limits_{0}^{5}{\left| \left| {{x}^{2}}-4x+3 \right|-x-3 \right|\,\text{d}x}=\int\limits_{0}^{5}{\left[ x+3-\left| {{x}^{2}}-4x+3 \right| \right]\,\text{d}x}\)
Ta có \(\int\limits_{0}^{5}{\left| {{x}^{2}}-4x+3 \right|\,\text{d}x}=\int\limits_{0}^{1}{\left| {{x}^{2}}-4x+3 \right|\,\text{d}x}+\int\limits_{1}^{3}{\left| {{x}^{2}}-4x+3 \right|\,\text{d}x}+\int\limits_{3}^{5}{\left| {{x}^{2}}-4x+3 \right|\,\text{d}x}\)
\(=\int\limits_{0}^{1}{\left( {{x}^{2}}-4x+3 \right)\,\text{d}x}-\int\limits_{1}^{3}{\left( {{x}^{2}}-4x+3 \right)\,\text{d}x}+\int\limits_{3}^{5}{\left( {{x}^{2}}-4x+3 \right)\,\text{d}x}=\frac{4}{3}-\left( -\,\frac{4}{3} \right)+\frac{20}{3}=\frac{28}{3}.\)
Vậy \(S=\int\limits_{0}^{5}{\left( x+3 \right)\,\text{d}x}-\frac{28}{3}=\left. \left( \frac{{{x}^{2}}}{2}+3x \right) \right|_{0}^{5}-\frac{28}{3}=\frac{109}{6}.\)
Đáp án cần chọn là: b
Toán Lớp 12
