Lời giải của Tự Học 365

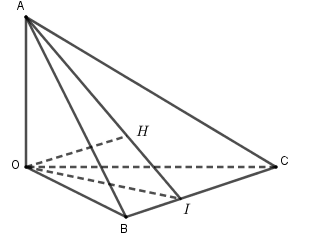
Ta có \(OA \bot (OBC) \Rightarrow OA \bot BC\), mà \(OH \bot BC\) \( \Rightarrow BC \bot (OAH) \Rightarrow BC \bot AH\).

Tương tự, ta có \(AB \bot CH\), suy ra đáp án A đúng.

Gọi \(I = AH \cap BC\)

Ta có \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\) \( \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{9} + \dfrac{1}{9} + \dfrac{1}{9} \Rightarrow O{H^2} = 3 \Leftrightarrow OH = \sqrt 3 \), suy ra đáp án C đúng.

Ngoài ra các tam giác \(OAB,OBC,OAC\) bằng nhau nên \(AB = BC = CA\) hay tam giác \(ABC\) đều, từ đó \(H\) là trực tâm của tam giác nên B đúng.

Đáp án cần chọn là: d