Cho hình chóp $S.ABC$ có $\widehat {BSC} = {120^0},\widehat {CSA} = {60^0},\widehat {ASB} = {90^0},$ $SA = SB = SC.$ Gọi $I$ là hình chiếu vuông góc của $S$ lên $mp\left( {ABC} \right).$ Chọn khẳng định đúng trong các khẳng định sau
Phương pháp giải
- Sử dụng định lý Pi-ta-go đảo và định lý hàm số cos để chứng minh \(\Delta ABC\) vuông tại \(A\).
- Sử dụng định nghĩa trục đường tròn đáy để tìm hình chiếu của \(S\) trên mặt đáy.
Lời giải của Tự Học 365
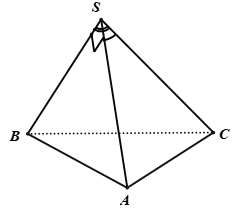
Gọi \(SA = SB = SC = a\)
Ta có :$\vartriangle SAC$ đều \( \Rightarrow AC = SA = a\)
$\vartriangle SAB$ vuông cân tại $S$ \( \Rightarrow AB = a\sqrt 2 \)
\(BC = \sqrt {S{B^2} + S{C^2} - 2SB.SC.\cos \widehat {BSC}} = a\sqrt 3 \)
$\vartriangle ABC$ vuông tại $A$
Gọi $I$ là trung điểm của $AC$ thì là tâm đường tròn
ngoại tiếp tam giác $ABC.$
Do \(SA = SB = SC\) và \(IA = IB = IC\) nên \(SI \bot \left( {ABC} \right)\).
Vậy \(I\) là hình chiếu vuông góc của $S$ lên mặt phẳng $\left( {ABC} \right)$
Đáp án cần chọn là: d
Toán Lớp 12
