Cho hình tứ diện \(ABCD\) có $AB$, $BC$, $CD$ đôi một vuông góc nhau. Hãy chỉ ra điểm \(O\) cách đều bốn điểm \(A\), \(B\), \(C\), \(D\).
Phương pháp giải
- Chứng minh tứ diện \(ABCD\) có cả bốn mặt đều là các tam giác vuông.
- Dùng tính chất của tam giác vuông : Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền để kết luận.
Lời giải của Tự Học 365
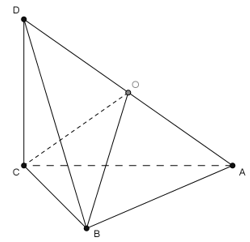
Gọi \(O\) là trung điểm của \(AD\).
Từ giả thiết ta có \(\left\{ \begin{array}{l}AB \bot CD\\BC \bot CD\end{array} \right. \Rightarrow CD \bot \left( {ABC} \right) \Rightarrow CD \bot AC\). Vậy $\Delta ACD$ vuông tại \(C\).
Do đó \(OA = OC = OD\) (1)
Mặt khác \(\left\{ \begin{array}{l}AB \bot CD\\AB \bot BC\end{array} \right. \Rightarrow AB \bot \left( {BCD} \right) \Rightarrow AB \bot BD \Rightarrow \Delta ABD\) vuông tại \(B\).
Do đó \(OA = OB = OD\) (2)
Từ (1) và (2) ta có \(OA = OB = OC = OD\).
Đáp án cần chọn là: d
Toán Lớp 12
