Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi \(I\), \(J\), \(K\) lần lượt là trung điểm của \(AB\), \(BC\) và \(SB\). Khẳng định nào sau đây sai?
Phương pháp giải
Sử dụng các cách chứng minh đường thẳng vuông góc mặt phẳng, mặt phẳng song song mặt phẳng để xét tính đúng, sai của các đáp án.
Lời giải của Tự Học 365
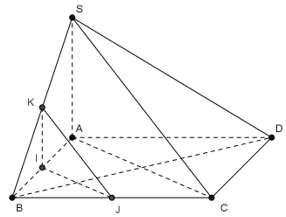
Do \(IJ\;{\rm{//}}\;AC\) và \(IK{\rm{//}}SA\) nên \(\left( {IJK} \right){\rm{//}}\left( {SAC} \right)\). Vậy A đúng.
Do \(BD \bot AC\) và \(BD \bot SA\) nên \(BD \bot \left( {SAC} \right)\) nên D đúng.
Do \(BD \bot \left( {SAC} \right)\) và \(\left( {IJK} \right){\rm{//}}\left( {SAC} \right)\) nên \(BD \bot \left( {IJK} \right)\) nên B đúng.
Vậy C sai.
Đáp án cần chọn là: c
Toán Lớp 12
