Cho hai hình chữ nhật $ABCD$ và $ABEF$ nằm trong hai mặt phẳng khác nhau sao cho hai đường thẳng $AC$ và $BF$ vuông góc với nhau. Gọi $CH$ và $FK$ lần lượt là đường cao của hai tam giác $BCE$ và $ADF$.
Khẳng định nào sau đây là sai?
Phương pháp giải
"/lop-11/chi-tiet-ly-thuyet-bai-tap-duong-thang-vuong-goc-voi-mat-phang-5af3eae81261631175a05d1d.html#d2">Chứng minh hai đường thẳng vuông góc bằng cách chứng minh đường thẳng vuông góc mặt phẳng
Lời giải của Tự Học 365
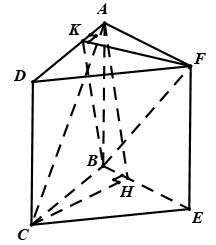
Ta có $\left. \begin{array}{l}AB \bot BC\\AB \bot BE\end{array} \right\} \Rightarrow AB \bot \left( {BCE} \right)$
Vậy $\left\{ \begin{array}{l}CH \bot AB\\CH \bot BE\end{array} \right. \Rightarrow CH \bot \left( {ABEF} \right)$
Ta có $CH \bot \left( {ABEF} \right) \Rightarrow CH \bot BF$, mặt khác $AC \bot BF \Rightarrow BF \bot \left( {ACH} \right) \Rightarrow BF \bot AH$.
Tương tự $\left. \begin{array}{l}AC \bot KF\\AC \bot BF\end{array} \right\} \Rightarrow AC \bot \left( {BKF} \right) \Rightarrow AC \bot BK$.
Đáp án cần chọn là: b
Toán Lớp 12
