Cho hình chóp $SABC$ có $SA \bot \left( {ABC} \right).$ Gọi $H,{\rm{ }}K$ lần lượt là trực tâm các tam giác $SBC$ và$ABC$. Mệnh đề nào sai trong các mệnh đề sau?
Phương pháp giải
Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để xét tính đúng, sai của các đáp án.
Lời giải của Tự Học 365
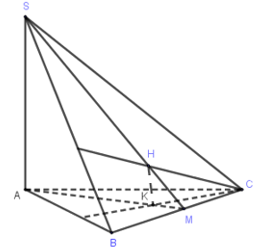
Ta có\(BC \bot SA,\,BC\, \bot SH\,\, \Rightarrow \,BC \bot (SAH)\)
Ta có \(CK \bot AB,CK \bot SA \Rightarrow CK \bot (SAB)\) hay \(CK \bot SB\)
Mặt khác có \(CH \bot SB\) nên \(SB \bot (CHK)\) hay \(SB \bot HK\), tương tự \(SC \bot HK\) nên \(HK\, \bot (SBC)\)
Gọi \(M\) là giao điểm của \(SH\) và \(BC\). Do \(BC \bot (SAH)\,\, \Rightarrow BC \bot AM\) hay đường thẳng
\(AM\) trùng với đường thẳng \(AK\). Hay $SH,AK$ và $BC$ đồng quy.
Do đó $BC \bot \left( {SAB} \right)$ là sai.
Đáp án cần chọn là: c
Toán Lớp 12
