Lời giải của Tự Học 365

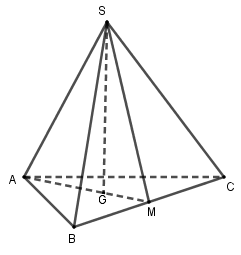
Vì \(SA = SB = SC\) và \(G\) là trọng tâm tam giác \(ABC\)

Suy ra \(G\) là chân đường cao kẻ từ đỉnh \(S\) xuống mặt phẳng \(\left( {ABC} \right).\)

Gọi \(M\) là trung điểm của \(BC\) suy ra \(BM = CM = \dfrac{{BC}}{2} = \dfrac{a}{2}.\)

Tam giác \(ABC\) đều cạnh \(a,\) có \(GM = \dfrac{{AM}}{3} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{1}{3} = \dfrac{{a\sqrt 3 }}{6}.\)

Tam giác \(SBM\) vuông tại \(M,\) có \(SM = \sqrt {S{B^2} - M{B^2}}  = \sqrt {{b^2} - \dfrac{{{a^2}}}{4}} .\)

Tam giác \(SGM\) vuông tại \(G,\) có \(SG = \sqrt {S{M^2} - G{M^2}}  = \sqrt {{b^2} - \dfrac{{{a^2}}}{4} - \dfrac{{{a^2}}}{{12}}}  = \dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}.\)

Đáp án cần chọn là: c