Trong mặt phẳng tọa độ $Oxy$, tam giác $ABC$ có đỉnh \(A\left( { - 1;2} \right)\), trực tâm \(H\left( { - 3; - 12} \right)\), trung điểm của cạnh $BC$ là \(M\left( {4;3} \right)\). Gọi $I$, $R$ lần lượt là tâm, bán kính đường tròn ngoại tiếp tam giác $ABC$. Chọn khẳng định đúng trong các khẳng định sau
Phương pháp giải
- Dựng hình, sử dụng kiến thức hình học lớp 9 tìm tọa độ điểm \(I\) suy ra bán kính.
Lời giải của Tự Học 365
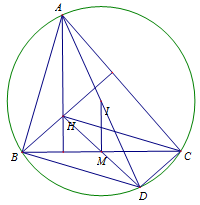
Kẻ đường kính \(AD\) của đường tròn \(\left( I \right)\) khi đó ta có \(BHCD\) là hình bình hành
\( \Rightarrow \)\(M\) là trung điểm của cạnh \(HD\).
Xét tam giác \(AHD\) có \(IM\) là đường trung bình \( \Rightarrow IM = \dfrac{1}{2}AH\) \( \Rightarrow \overrightarrow {IM} = \dfrac{1}{2}\overrightarrow {AH} \).
Gọi \(I\left( {x;y} \right)\) ta có \(\overrightarrow {IM} = \left( {4 - x;3 - y} \right)\); \(\overrightarrow {AH} = \left( { - 2; - 14} \right)\) \( \Rightarrow I\left( {5;10} \right)\).
Bán kính \(R = IA = \sqrt {{{\left( {5 + 1} \right)}^2} + {{\left( {10 - 2} \right)}^2}} = 10\)
Đáp án cần chọn là: d
Toán Lớp 12
