Lời giải của Tự Học 365

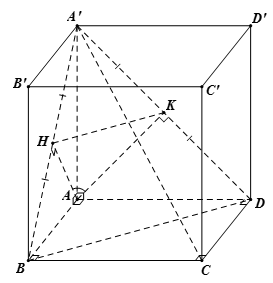
Ta có: \(AH \bot \left( {BA'C} \right),\,AK \bot \left( {DA'C} \right)\) với \(H,\,K\) lần lượt là trung điểm của \(A'B,\,A'D\)

Suy ra $\widehat {\left( {\left( {BA'C} \right);\left( {DA'C} \right)} \right)} = \widehat {\left( {AH;AK} \right)} = \widehat {HAK}$

Lại có: \(HK\) là đường trung bình của \(\Delta A'BD\) nên \(HK = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\)

Mặt khác: \(AH = AK = \dfrac{{a\sqrt 2 }}{2}\)

Do đó \(AH = AK = HK = a\sqrt 2 \)

Suy ra \(\Delta AHK\) đều

Vậy $\widehat {\left( {\left( {BA'C} \right);\left( {DA'C} \right)} \right)} = \widehat {HAK} = 60^\circ $.

Đáp án cần chọn là: a