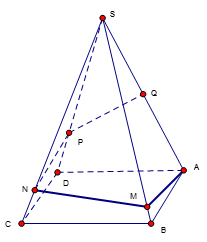
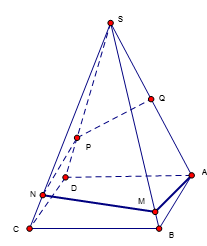
Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều $S.ABCD$ cạnh bên $SA = 600$ mét, $\widehat {ASB} = 15^\circ $. Do có sự cố đường dây điện tại điểm $Q$ (là trung điểm của $SA$) bị hỏng, người ta tạo ra một con đường từ $A$ đến $Q$ gồm bốn đoạn thẳng: $AM$, $MN$, $NP$, $PQ$ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và có được chiều dài con đường từ $A$ đến $Q$ ngắn nhất. Tính tỉ số $k = \dfrac{{AM + MN}}{{NP + PQ}}$.
Phương pháp giải
Trải phẳng khối đa diện và đánh giá GTNN của tổng \(AM + MN + NP + PQ\), từ đó suy ra vị trí điểm \(N\) và kết luận.
Lời giải của Tự Học 365
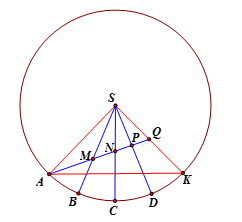
Giả sử trải các mặt hình chóp đều trên đường tròn tâm \(S\) và bán kính \(R = SA\). Ta có \(\Delta SAK\) có $\widehat {ASK} = 15^\circ .4 = 60^\circ $ $ \Rightarrow \Delta SAK$ đều.
Mà đoạn đường \(AQ\) ngắn nhất khi \(A\), \(M\), \(N\), \(P\), \(Q\) thẳng hàng.
Khi đó \(N\) là trọng tâm \(\Delta SAK\). Suy ra $k = \dfrac{{AM + MN}}{{NP + PQ}} = \dfrac{{AN}}{{NQ}} = 2$.
Đáp án cần chọn là: a
Toán Lớp 12
