Cho hình đa diện SABCD có $SA = 4,\,\,SB = 2,\,\,SC = 3,\,\,SD = 1$ và $\widehat {ASB} = \widehat {BSC} = \widehat {CSD} = \widehat {DSA} = {60^0}$. Khoảng cách từ điểm A tới mặt phẳng $(SCD)$ là:
Phương pháp giải
- Trên các tia SA, SB, SC lần lượt lấy các điểm A’, B’, C’ sao cho SA’=SB’=SC’=1.
- Chứng minh SA’B’C’D là chóp tứ giác đều.
- Tính khoảng cách từ A đến (SCD) thông qua khoảng cách từ A’ đến (SC’D).
Lời giải của Tự Học 365
Chóp tứ giác S.ABCD có: $SA' = SB' = SC' = SD = 1$ và $\widehat {A'SB'} = \widehat {B'SC'} = \widehat {C'SD} = \widehat {DSA'} = {60^0}$
$ \Rightarrow S.A'B'C'D$ là chóp tứ giác đều.
+) Tính khoảng cách từ A’ đến (SC’D):
$\left\{ \begin{array}{l}A'C' \cap (SC'D) = C'\\A'C' = 2.OC'\end{array} \right. \Rightarrow d(A';(SC'D)) = 2.d(O;(SC'D))$
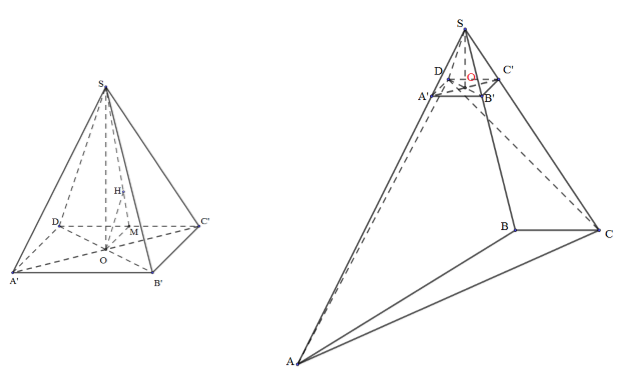
Ta có : $OM = \dfrac{{A'D}}{2} = \dfrac{1}{2}$, $OC = \dfrac{{\sqrt 2 }}{2}.1 = \dfrac{{\sqrt 2 }}{2}$
$\Delta SOC'$ vuông tại O $ \Rightarrow SO = \sqrt {SC{'^2} - OC{'^2}} = \sqrt {1 - {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{\sqrt 2 }}{2}$
$\Delta SOM$ vuông tại O, $OH \bot SM \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}} = \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{1}{2}} \right)}^2}}} = 6 \Rightarrow OH = \dfrac{1}{{\sqrt 6 }}$
$ \Rightarrow d(O;(SC'D)) = \dfrac{1}{{\sqrt 6 }} \Rightarrow d(A';(SC'D)) = \dfrac{2}{{\sqrt 6 }}$
+) Vì $\left\{ \begin{array}{l}SA \cap (SC'D) = C'\\SA = 4.SA'\end{array} \right. \Rightarrow d(A;(SC'D)) = 4.d(A';(SC'D)) = 4.\dfrac{2}{{\sqrt 6 }} = \dfrac{8}{{\sqrt 6 }} = \dfrac{{4\sqrt 6 }}{3}$
Vậy, khoảng cách từ A đến (SCD) là $\dfrac{{4\sqrt 6 }}{3}$.
Đáp án cần chọn là: b
Toán Lớp 12
