Lời giải của Tự Học 365

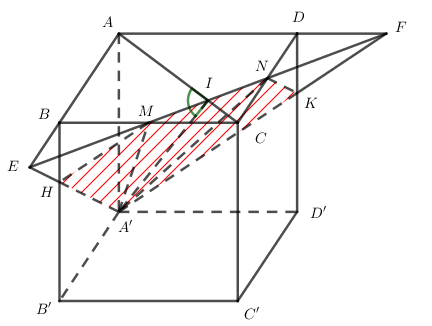
Kéo dài MN cắt AB và AD lần lượt tại E và F.

Gọi \(H = A'E \cap BB';\,\,K = A'F \cap DD'\). Khi đó thiết diện là A’HMNK.

Ta có ABMND là hình chiếu của A’HMNK trên mặt phẳng \(\left( {ABCD} \right)\).

Gọi \(I = AC \cap MN\) ta có: \(AC \bot BD;\,\,MN//BD \Rightarrow AC \bot MN\) tại I.

\(\left\{ \begin{array}{l}MN \bot AI\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {A'AI} \right) \Rightarrow MN \bot A'I\)

\( \Rightarrow \widehat {\left( {\left( {A'HMNK} \right);\left( {ABCD} \right)} \right)} = \widehat {AIA'}\)

Ta có :

\(CM = CN = 1 \Rightarrow MN = \sqrt 2  \Rightarrow IC = \dfrac{{\sqrt 2 }}{2}\)

\(AC = 2\sqrt 2  \Rightarrow AI = 2\sqrt 2  - \dfrac{{\sqrt 2 }}{2} = \dfrac{{3\sqrt 2 }}{2}\).

Xét tam giác vuông AA’I có: \(A'I = \sqrt {AA{'^2} + A{I^2}}  = \sqrt {4 + \dfrac{9}{2}}  = \dfrac{{\sqrt {34} }}{2}\).

\( \Rightarrow \cos \widehat {AIA'} = \dfrac{{AI}}{{A'I}} = \dfrac{{\dfrac{{3\sqrt 2 }}{2}}}{{\dfrac{{\sqrt {34} }}{2}}} = \dfrac{3}{{\sqrt {17} }} = \cos \widehat {\left( {\left( {ABCD} \right);\left( {A'HMNK} \right)} \right)}\)

Ta có \({S_{ABCD}} = 4;\,\,{S_{CMN}}\dfrac{1}{2}.1.1 = \dfrac{1}{2} \Rightarrow {S_{ABMND}} = 4 - \dfrac{1}{2} = \dfrac{7}{2}\)

$ \Rightarrow {S_{A'HMNK}} = \dfrac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}} = \dfrac{7}{2}.\dfrac{{\sqrt {17} }}{3} = \dfrac{{7\sqrt {17} }}{6}$ .

Đáp án cần chọn là: a