Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều \(S.ABCD\) cạnh bên bằng \(200{\mathop{\rm m} olimits} \), góc $\widehat {ASB} = 15^\circ $ bằng đường gấp khúc dây đèn Led vòng quanh kim tự tháp \(AEFGHIJKLS\). Trong đó điểm \(L\) cố định và \(LS = 40{\mathop{\rm m} olimits} \). Hỏi khi đó cần dùng ít nhất bao nhiêu mét dây đèn Led để trang trí?
Phương pháp giải
Trải hình chóp \(S.ABCD\) ra mặt phẳng hai lần, đánh giá tổng chiều dài dây ngắn nhất.
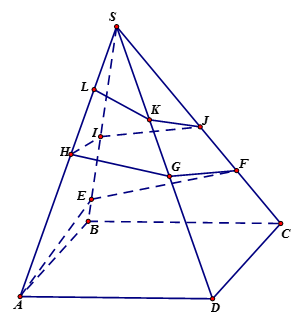
Lời giải của Tự Học 365
Ta sử dụng phương pháp trải đa diện
Cắt hình chóp theo cạnh bên \(SA\) rồi trải ra mặt phẳng hai lần, ta có hình vẽ sau
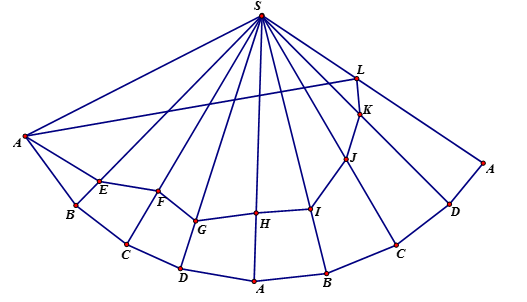
Từ đó suy ra chiều dài dây đèn led ngắn nhất là bằng $AL + LS$.
Từ giả thiết về hình chóp đều \(S.ABCD\)ta có \(\widehat {ASL} = 120^\circ \).
Ta có \(A{L^2} = S{A^2} + S{L^2} - 2SA.SL.\cos \widehat {ASL} = {200^2} + {40^2} - 2.200.40.\cos 120^\circ = 49600\).
Nên \(AL = \sqrt {49600} = 40\sqrt {31} \).
Vậy, chiều dài dây đèn led cần ít nhất là \(40\sqrt {31} + 40\) mét.
Đáp án cần chọn là: c
Toán Lớp 12
