Lời giải của Tự Học 365

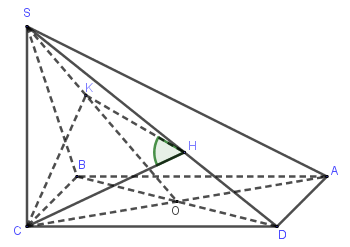
Từ $SC \bot \left( {ABCD} \right) \Rightarrow SC \bot BD$.

Từ $\left\{ \begin{array}{l}BD \bot SC\\BD \bot AC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)$.

Kẻ $CK \bot SO$, từ $BD \bot \left( {SAC} \right) \Rightarrow BD \bot CK$. Như vậy $CK \bot \left( {SBD} \right) \Rightarrow CK \bot SD$.

Kẻ $CH \bot SD$, do $CK \bot SD$ nên suy ra $SD \bot \left( {CHK} \right)$.

Mặt khác $\left( {CHK} \right) \cap \left( {SBD} \right) = HK$ và $\left( {CHK} \right) \cap \left( {SCD} \right) = CK$ nên góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$ bằng $\widehat {CHK}$.

Trong tam giác $SCD$ vuông tại $C$, ta có:

$\dfrac{1}{{C{H^2}}} = \dfrac{1}{{C{D^2}}} + \dfrac{1}{{S{C^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{2}} \right)}^2}}} = \dfrac{5}{{3{a^2}}} \Rightarrow CH = \dfrac{{a\sqrt 3 }}{{\sqrt 5 }}$.

Vì $ABCD$ là hình thoi cạnh bằng $a$ và góc $A$ bằng $60^\circ$ nên $CO = \dfrac{{a\sqrt 3 }}{2}$.

Trong tam giác $SCO$ vuông tại $C$, ta có:

$\dfrac{1}{{C{K^2}}} = \dfrac{1}{{C{O^2}}} + \dfrac{1}{{S{C^2}}} = \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{2}} \right)}^2}}} = \dfrac{2}{{{a^2}}} \Rightarrow CK = \dfrac{a}{{\sqrt 2 }}$.

Xét tam giác $CHK$ vuông tại $K$, ta có

$HK = \sqrt {C{H^2} - C{K^2}}  = \sqrt {\dfrac{{3{a^2}}}{5} - \dfrac{{{a^2}}}{2}}  = \dfrac{a}{{\sqrt {10} }}$.

$\cos \widehat {CHK} = \dfrac{{HK}}{{CH}} = \dfrac{a}{{\sqrt {10} }}:\dfrac{{a\sqrt 3 }}{{\sqrt 5 }} = \dfrac{{\sqrt 6 }}{6}$.

Vậy, cô-sin của góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$ bằng $\dfrac{{\sqrt 6 }}{6}$.

Đáp án cần chọn là: a