Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với đáy, \(SA = 2BC\) và \(\widehat {BAC} = 120^\circ \). Hình chiếu vuông góc của \(A\) lên các đoạn \(SB\) và \(SC\) lần lượt là \(M\) và \(N\). Góc của hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AMN} \right)\) bằng
Phương pháp giải
- Xác định góc giữa hai mặt phẳng, sử dụng lý thuyết: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Chú ý: Kẻ đường kính \(AD\) của đường tròn ngoại tiếp \(\Delta ABC\).
- Tính góc dựa vào các kiến thức hình học đã biết.
Lời giải của Tự Học 365
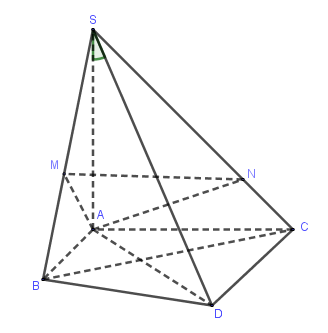
Kẻ đường kính \(AD\) của đường tròn ngoại tiếp \(\Delta ABC\) nên \(\widehat {ABD} = \widehat {ACD} = 90^\circ \).
Ta có \(\left\{ \begin{array}{l}BD \bot BA\\BD \bot SA\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAB} \right)\) hay \(BD \bot AM\) và \(AM \bot SB\) hay $AM \bot \left( {SBD} \right)$\( \Rightarrow AM \bot SD\). Chứng minh tương tự ta được \(AN \bot SD\). Suy ra \(SD \bot \left( {AMN} \right)\), mà \(SA \bot \left( {ABC} \right)\) \( \Rightarrow \left( {\left( {ABC} \right),\left( {AMN} \right)} \right) = \left( {SA,SD} \right) = \widehat {DSA}\).
Ta có \(BC = 2R\sin A\)\( = AD.\dfrac{{\sqrt 3 }}{2}\)\( \Rightarrow SA = 2BC = AD\sqrt 3 \).
Vậy $\tan \widehat {ASD} = \dfrac{{AD}}{{SA}}$$ = \dfrac{1}{{\sqrt 3 }}$$ \Rightarrow \widehat {ASD} = 30^\circ $.
Đáp án cần chọn là: d
Toán Lớp 12
