Lời giải của Tự Học 365

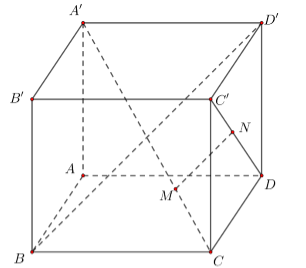
Đặt \(\overrightarrow {AB}  = \vec a\), \(\overrightarrow {AD}  = \vec b\), $\overrightarrow {AA'}  = \vec c$.

Từ \(\overrightarrow {MA'}  = k.\overrightarrow {MC} \) \( \Rightarrow \overrightarrow {AA'}  - \overrightarrow {AM}  = k\left( {\overrightarrow {AC}  - \overrightarrow {AM} } \right)\) \( \Rightarrow \overrightarrow {AM}  = \dfrac{{\overrightarrow {AA'}  - k\overrightarrow {AC} }}{{1 - k}} = \dfrac{{ - k\left( {\vec a + \vec b} \right) + \vec c}}{{1 - k}}\).

và \(\overrightarrow {NC'}  = l.\overrightarrow {ND} \) $ \Rightarrow \overrightarrow {AC'}  - \overrightarrow {AN}  = l.\left( {\overrightarrow {AD}  - \overrightarrow {AN} } \right)$\( \Leftrightarrow \overrightarrow {AN}  = \dfrac{{\overrightarrow {AC'}  - l\overrightarrow {AD} }}{{1 - l}} = \dfrac{{\vec a + \vec b + \vec c - l\vec b}}{{1 - l}}\).

Vậy $\overrightarrow {MN}  = \overrightarrow {AM}  - \overrightarrow {AN} $\( = \dfrac{{ - k\left( {\vec a + \vec b} \right) + \vec c}}{{1 - k}} - \dfrac{{\vec a + \vec b + \vec c - l\vec b}}{{1 - l}}\)

\( = \left( { - \dfrac{k}{{1 - k}} - \dfrac{1}{{1 - l}}} \right)\vec a + \left( { - \dfrac{k}{{1 - k}} - 1} \right)\vec b + \left( {\dfrac{1}{{1 - k}} - \dfrac{1}{{1 - l}}} \right)\vec c\).

Mặt khác, $\overrightarrow {BD'}  = \overrightarrow {AD'}  - \overrightarrow {AB}  =  - \vec a + \vec b + \vec c$.

Để \(MN{\rm{//}}BD'\) thì $\overrightarrow {MN} {\rm{//}}\overrightarrow {BD'} $ \( \Rightarrow \left\{ \begin{array}{l}\dfrac{k}{{1 - k}} + \dfrac{1}{{1 - l}} =  - \dfrac{k}{{1 - k}} - 1\\ - \dfrac{k}{{1 - k}} - 1 = \dfrac{1}{{1 - k}} - \dfrac{1}{{1 - l}}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2k}}{{1 - k}} + \dfrac{1}{{1 - l}} =  - 1\\\dfrac{{k + 1}}{{1 - k}} - \dfrac{1}{{1 - l}} =  - 1\end{array} \right.\)

\( \Rightarrow \dfrac{{3k + 1}}{{1 - k}} =  - 2\) \( \Leftrightarrow k =  - 3\). Từ đó ta có: \(\dfrac{1}{{1 - l}} = \dfrac{1}{2}\) \( \Rightarrow l =  - 1\).

Vậy \(k + l =  - 4\).

Đáp án cần chọn là: c