Lời giải của Tự Học 365

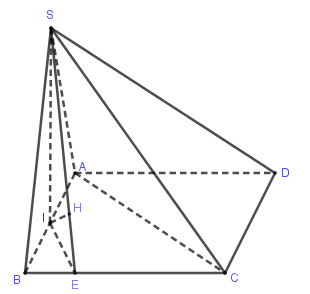
Gọi \(I\) là trung điểm \(AB\). Khi đó, ta có: \(SI \bot \left( {ABCD} \right)\).

Do \(AD{\rm{//}}BC\) nên\(d\left( {AD,SC} \right) = d\left( {AD,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right) = 2d\left( {I,\left( {SBC} \right)} \right)\)

Xét \(\Delta ABD\) có \(DI\) là trung tuyến nên \(DI = \sqrt {\dfrac{{D{A^2} + D{B^2}}}{2} - \dfrac{{A{B^2}}}{4}}  = \dfrac{{a\sqrt 7 }}{2}\).

Suy ra \(SI = DI.\tan 60^\circ  = \dfrac{{a\sqrt {21} }}{2}\).

Từ \(I\) kẻ \(IE\) vuông góc với \(BC\). Từ \(I\) kẻ \(IH\) vuông góc với \(SE\). Khi đó, ta chứng minh được \(IH = d\left( {I,\left( {SBC} \right)} \right)\).

Do \(I\) là trung điểm \(AB\) trong \(\Delta ABC\) đều nên \(IE = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}\).

Vậy \(\dfrac{1}{{I{H^2}}} = \dfrac{1}{{I{S^2}}} + \dfrac{1}{{I{E^2}}} = \dfrac{{116}}{{21{a^2}}}\) hay \(IH = \dfrac{{\sqrt {609} }}{{58}}\).

Kết luận: \(d\left( {AD,SC} \right) = \dfrac{{\sqrt {609} }}{{29}}\).

Đáp án cần chọn là: b