Lời giải của Tự Học 365

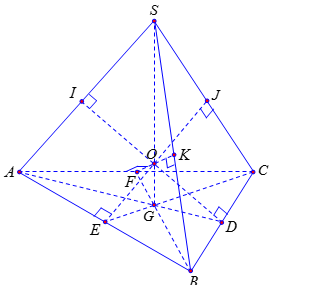
Ta có khối chóp $S.ABC$ là khối chóp tam giác đều.

Gọi $G$ là trọng tâm tam giác $ABC$. Khi đó $SG$ là chiều cao của khối chóp $S.ABC$.

Gọi $D$,$E$,$F$lần lượt là trung điểm của $BC$,$AB$,$CA$ và $I$,$J$,$K$ lần lượt là hình chiếu của $D$,$E$,$F$ trên $SA$,$SC$,$SB$.

Khi đó $DI$,$EJ$,$FK$tương ứng là các đường vuông góc chung của các cặp cạnh $SA$ và $BC$, $SC$ và $AB$, $SB$ và $CA$.

Ta có $DI = EJ = FK$. Do đó $\Delta SID = \Delta SJE$ nên $SI = SJ$.

Suy ra $ED//IJ$ (cùng song song với \(AC\)). Do đó bốn điểm $D$,$E$,$I$,$J$ đồng phẳng.

Tương tự ta có bộ bốn điểm $D$,$F$,$I$,$K$ và $E$,$F$,$J$,$K$ đồng phẳng.

Ba mặt phẳng $\left( {DEIJ} \right)$,$\left( {DFIK} \right)$,$\left( {EFJK} \right)$ đôi một cắt nhau theo ba giao tuyến $DI$, $EJ$, $FK$. Suy ra $DI$,$EJ$,$FK$ đồng quy tại điểm $O$ thuộc $SG$.

Xét điểm $M$bất kì trong không gian.

Ta có $\left\{ \begin{array}{l}d\left( {M,SA} \right) + d\left( {M,BC} \right) \ge DI\\d\left( {M,SC} \right) + d\left( {M,AB} \right) \ge EJ\\d\left( {M,SB} \right) + d\left( {M,AC} \right) \ge FK\end{array} \right. \Rightarrow d \ge DI + EJ + FK$.

Do đó \(d\) nhỏ nhất bằng $DI + EJ + FK = 3DI$ khi $M \equiv O$.

Ta có $AD = \dfrac{{a\sqrt 3 }}{2}$, \(AG = \dfrac{2}{3}AD = \dfrac{{a\sqrt 3 }}{3}\), $SG = \sqrt {S{A^2} - A{G^2}}  = \dfrac{{2a\sqrt 6 }}{3}$, $\sin \widehat {SAG} = \dfrac{{SG}}{{SA}} = \dfrac{{2\sqrt 2 }}{3}$.

Suy ra $DI = AD.\sin \widehat {SAD} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{2\sqrt 2 }}{3} = \dfrac{{a\sqrt 6 }}{3}$.

Vậy giá trị nhỏ nhất cần tìm là $3DI = 3\dfrac{{a\sqrt 6 }}{3} = a\sqrt 6 $.

Đáp án cần chọn là: c