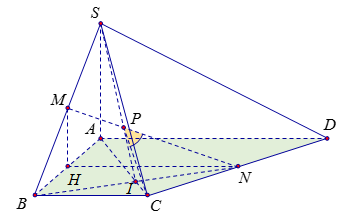
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\) và có \(AB = BC = a\), \(AD = 2a\), có \(SA\) vuông góc với đáy và \(SA = a\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(SB\) và \(CD\). Tính \({\rm{cosin}}\) của góc giữa \(MN\) và \(\left( {SAC} \right)\).
Phương pháp giải
- Xác định giao điểm của \(MN\) và \(\left( {SAC} \right)\).
- Xác định góc $\widehat {\left( {MN,\left( {SAC} \right)} \right)}$ và tính góc đó
Lời giải của Tự Học 365
Xác định giao điểm của \(MN\) và \(\left( {SAC} \right)\):
ü Chọn mp chứa \(MN\) là mp\(\left( {SBN} \right)\)
ü Giao tuyến \(\left( {SBN} \right) \cap \left( {SAC} \right) = SI\) (với \(I = AC \cap BN\)
Trong \(\left( {SBN} \right)\) gọi \(SI \cap MN = P\), suy ra \(P = MN \cap \left( {SAC} \right)\).
Xác định góc $\widehat {\left( {MN,\left( {SAC} \right)} \right)}$- Ta có \(A{C^2} = A{B^2} + B{C^2} = 2{a^2}\); \(C{D^2} = C{K^2} + K{D^2} = 2{a^2}\); \(A{D^2} = {\left( {2a} \right)^2} = 4{a^2}\) \( \Rightarrow A{C^2} + C{D^2} = A{D^2}\) \( \Rightarrow \Delta ACD\) vuông tại \(C\) \( \Rightarrow CD \bot AC\) mà \(CD \bot SA\) nên \(CD \bot \left( {SAC} \right)\)
- Góc $\widehat {\left( {MN,\left( {SAC} \right)} \right)} = \widehat {\left( {MN,PC} \right)} = \widehat {NPC}$
 Tính góc \(\widehat {NPC}\):
Tính góc \(\widehat {NPC}\):
ü Ta có \(NC = \dfrac{{CD}}{2} = \dfrac{{a\sqrt 2 }}{2}\).
ü Ta có \(I\) là trung điểm \(BN\) và \(M\) là trung điểm \(SB\) suy ra \(P\) là trọng tâm \(\Delta SBN\) \( \Rightarrow PN = \dfrac{2}{3}MN\)
ü Gọi \(H\) trung điểm \(AB\) suy ra \(MH{\rm{//}}SA\) do đó \(\Delta MNH\) vuông tại \(H\). $ \Rightarrow MN = \sqrt {M{H^2} + H{N^2}} $ $ = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a + 2a}}{2}} \right)}^2}} = \dfrac{{a\sqrt {10} }}{2}$ do đó \(PN = \dfrac{2}{3}MN = \dfrac{{a\sqrt {10} }}{3}\).
Từ đó suy ra $PC = \sqrt {P{N^2} - N{C^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt {10} }}{3}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{a\sqrt {22} }}{6}$
Cosin của góc \(\widehat {NPC}\): \(\cos \widehat {NPC} = \dfrac{{PC}}{{PN}} = \dfrac{{\dfrac{{a\sqrt {22} }}{6}}}{{\dfrac{{a\sqrt {10} }}{3}}} = \dfrac{{\sqrt {55} }}{{10}}\).Đáp án cần chọn là: b
Toán Lớp 12
