Cho hình hộp chữ nhật $ABCD.A'B'C'D'$, $AB = 6{\rm{cm}}$, $BC = BB' = 2{\rm{cm}}$. Điểm $E$ là trung điểm cạnh $BC$. Một tứ diện đều $MNPQ$ có hai đỉnh $M$ và $N$ nằm trên đường thẳng $C'E$, hai đỉnh $P$, $Q$ nằm trên đường thẳng đi qua điểm $B'$ và cắt đường thẳng $AD$ tại điểm $F$. Khoảng cách $DF$ bằng
Phương pháp giải
Sử dụng phương pháp véc tơ và tính chất tứ diện đều (hai cặp cạnh đối vuông góc) tìm vị trí điểm \(F\).
Lời giải của Tự Học 365
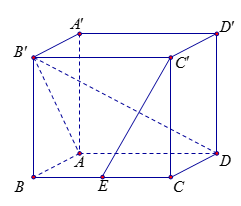
Do tứ diện $MNPQ$ đều nên ta có $MN \bot PQ$ hay $EC' \bot BF$.
Ta có: $\overrightarrow {B'F} = \overrightarrow {B'A} + \overrightarrow {AF} = \overrightarrow {B'A'} + \overrightarrow {B'B} + k\overrightarrow {AD} = \overrightarrow {B'A'} + \overrightarrow {B'B} + k\overrightarrow {B'C'} $
Và $\overrightarrow {EC'} = \overrightarrow {EC} + \overrightarrow {CC'} = \dfrac{1}{2}\overrightarrow {B'C'} - \overrightarrow {B'B} $
Khi đó, $\overrightarrow {EC'} .\overrightarrow {BF} = - B'{B^2} + \dfrac{k}{2}B'{C'^2} = - 4 + \dfrac{k}{2}.4 = 0$$ \Rightarrow k = 2$. Vậy $\overrightarrow {AF} = 2\overrightarrow {AD} $
Vậy $F$ là điểm trên $AD$ sao $D$ là trung điểm của $AF$.
Do đó $DF = BC = 2{\rm{cm}}$.
Đáp án cần chọn là: b
Toán Lớp 12
