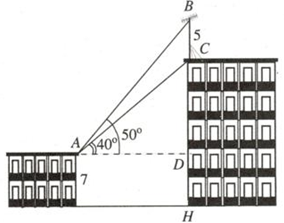
Trên nóc một tòa nhà có cột ăng-ten cao \(5\,{\rm{m}}\). Từ vị trí quan sát \(A\) cao \(7\,{\rm{m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang (như hình vẽ bên). Chiều cao của tòa nhà (được làm tròn đến hàng phần mười) là:
Phương pháp giải
- Tính độ dài \(CD\) bằng cách lập phương trình ẩn \(CD\) từ các điều kiện bài cho.
- Tính độ dài \(BC\) chính là chiều cao tòa nhà.
Lời giải của Tự Học 365
Ta có chiều cao của tòa nhà chính là đoạn \(BH\).
Mà \(BH = CD + DH\)\( = CD + 7\).
Xét tam giác \(ACD\) vuông tại \(D\) có \(AC = \dfrac{{CD}}{{\sin 40^\circ }}\)
Xét tam giác \(ABD\) vuông tại \(D\) có \(AB = \dfrac{{5 + CD}}{{\sin 50^\circ }}\)
Xét tam giác \(ABC\) có:
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\)
\( \Leftrightarrow \left( {\dfrac{1}{{{{\sin }^2}50^\circ }} + \dfrac{1}{{{{\sin }^2}40^\circ }} - \dfrac{{2\cos 10^\circ }}{{\sin 40^\circ \sin 50^\circ }}} \right)C{D^2} + \left( {\dfrac{{10}}{{{{\sin }^2}50^\circ }} - \dfrac{{10\cos 10^\circ }}{{\sin 40^\circ \sin 50^\circ }}} \right)CD + \dfrac{{25}}{{{{\sin }^2}50^\circ }} - 25 = 0\)\( \Leftrightarrow CD \approx 11,9\)
\( \Rightarrow BC \approx 7 + 11,9\)\( \approx 18,9\) (m).
Vậy tòa nhà cao \(18,9{\rm{ m}}\).
Đáp án cần chọn là: d
Toán Lớp 12
