Lời giải của Tự Học 365

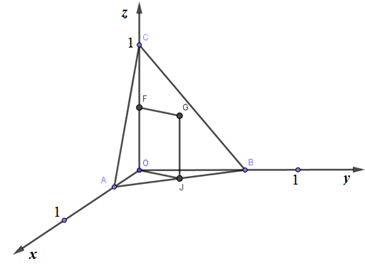
Đặt $A\left( {x;0;0} \right),\,\,B\left( {0;y;0} \right),\,\,\left( {x,y > 0} \right)$

Vì $OA + OB = OC = 1 \Rightarrow x + y = 1$

Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G.

$\Delta OAB$ vuông tại O $ \Rightarrow J$ là tâm đường tròn ngoại tiếp tam giác.

$GJ//OC \Rightarrow GJ \bot (OAB) \Rightarrow GO = GA = GB$

$GF//JO,\,\,JO \bot OC \Rightarrow GF \bot OC$, mà F là trung điểm của OC

$ \Rightarrow GF$ là đường trung trực của OC $ \Rightarrow GC = GO$

$ \Rightarrow GO = GA = GB = GC \Rightarrow G$ là tâm mặt cầu ngoại tiếp tứ diện OABC

Bán kính mặt cầu ngoại tiếp tứ diện OABC : $R = OG = FJ = \sqrt {O{F^2} + O{J^2}}  = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + O{J^2}} $

Ta có: $OJ = \dfrac{{AB}}{2} = \dfrac{{\sqrt {{x^2} + {y^2}} }}{2} \ge \dfrac{{\sqrt {\dfrac{{{{(x + y)}^2}}}{2}} }}{2} = \dfrac{{\sqrt {\dfrac{{{1^2}}}{2}} }}{2} = \dfrac{{\sqrt 2 }}{4}$$ \Rightarrow R \ge \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{{\sqrt 2 }}{4}} \right)}^2}}  = \sqrt {\dfrac{3}{8}}  \Rightarrow {R_{\min }} = \sqrt {\dfrac{3}{8}}  = \dfrac{{\sqrt 6 }}{4}$

Đáp án cần chọn là: c