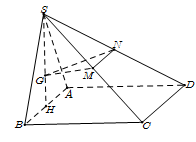
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\) mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng \((ABCD).\) Gọi \(G\) là trọng tâm của tam giác \(SAB\) và \(M,\,\,N\) lần lượt là trung điểm của \(SC,\,\,SD\) (tham khảo hình vẽ bên). Tính côsin của góc giữa hai mặt phẳng \((GMN)\) và \((ABCD).\)
Phương pháp giải
Gọi H là trung điểm của AB $ \Rightarrow \,\,SH \bot \left( {ABCD} \right).$
Gắn hệ tọa độ $Oxyz,$ với $H\left( {0;0;0} \right),\,\,S\left( {0;0;\dfrac{{\sqrt 3 }}{2}} \right),\,\,A\left( { - \dfrac{1}{2};0;0} \right);\,\,B\left( {\dfrac{1}{2};0;0} \right);\,\,C\left( {\dfrac{1}{2};1;0} \right),\,\,D\left( { - \dfrac{1}{2};1;0} \right)$
Gọi \({\overrightarrow n _1};{\overrightarrow n _2}\) lần lượt là các VTPT của mặt phẳng \(\left( {GMN} \right);\left( {ABCD} \right) \Rightarrow \cos \left( {\left( {GMN} \right);\left( {ABCD} \right)} \right) = \dfrac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}\)
Lời giải của Tự Học 365
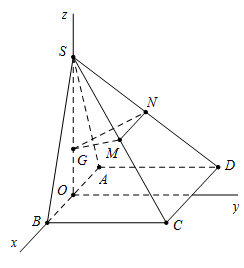
Gọi H là trung điểm của $AB.$ Vì $\left( {SAD} \right) \bot \left( {ABCD} \right)$$ \Rightarrow \,\,SH \bot \left( {ABCD} \right).$
Gắn hệ tọa độ $Oxyz,$ với $H\left( {0;0;0} \right),\,\,S\left( {0;0;\dfrac{{\sqrt 3 }}{2}} \right),\,\,A\left( { - \dfrac{1}{2};0;0} \right);\,\,B\left( {\dfrac{1}{2};0;0} \right);\,\,C\left( {\dfrac{1}{2};1;0} \right),\,\,D\left( { - \dfrac{1}{2};1;0} \right)$
Khi đó $G\left( {0;0;\dfrac{{\sqrt 3 }}{6}} \right),\,\,M\left( {\dfrac{1}{4};\dfrac{1}{2};\dfrac{{\sqrt 3 }}{4}} \right),\,\,N\left( { - \,\dfrac{1}{4};\dfrac{1}{2};\dfrac{{\sqrt 3 }}{4}} \right)$
$\begin{array}{l} \Rightarrow \overrightarrow {GM} = \left( {\dfrac{1}{4};\dfrac{1}{2};\dfrac{{\sqrt 3 }}{{12}}} \right);\,\,\overrightarrow {MN} = \left( { - \dfrac{1}{2};0;0} \right)\\ \Rightarrow \,\,{{\vec n}_1} = {{\vec n}_{\left( {GMN} \right)}} = \left[ {\overrightarrow {GM} ;\overrightarrow {MN} } \right] = \left( {0; - \dfrac{{\sqrt 3 }}{{24}};\dfrac{1}{4}} \right).\end{array}$
Và mặt phẳng $\left( {ABCD} \right)$ có vectơ pháp tuyến là ${\vec n_2} = {\vec n_{\left( {ABCD} \right)}} = \overrightarrow k = \left( {0;0;1} \right).$
Vậy cosin góc giữa hai mặt phẳng $\left( {GMN} \right),\,\,\left( {ABCD} \right)$ là $\cos \alpha = \dfrac{{\left| {{{\vec n}_1}.{{\vec n}_2}} \right|}}{{\left| {{{\vec n}_1}} \right|.\left| {{{\vec n}_2}} \right|}} = \dfrac{{2\sqrt {39} }}{{13}}.$
Đáp án cần chọn là: d
Toán Lớp 12
