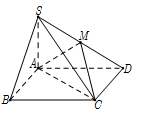
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\) cạnh bên \(SA\, = \,2a\) và vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(SD.\) Tang của góc tạo bởi hai mặt phẳng \((AMC)\) và \((SBC)\) bằng
Phương pháp giải
Tọa độ hóa bằng cách gắn hệ tọa độ Oxyz, áp dụng công thức tính góc giữa hai mặt phẳng
Lời giải của Tự Học 365
Gắn hệ tọa độ $Oxyz,$ với $A\left( {0;0;0} \right),\,\,S\left( {0;0;2} \right),\,\,D\left( {0;1;0} \right),\,\,B\left( {1;0;0} \right),\,\,C\left( {1;1;0} \right)$.
Tọa độ trung điểm $M$ của $SD$ là $M\left( {0;\dfrac{1}{2};1} \right).$ Ta có $\left[ {\overrightarrow {SB} ;\overrightarrow {SC} } \right] = \left( {2;0;1} \right)$ và $\left[ {\overrightarrow {AM} ;\overrightarrow {AC} } \right] = \left( { - \,1;1; - \,\dfrac{1}{2}} \right).$
Do đó $\cos \widehat {\left( {AMC} \right);\left( {SBC} \right)} = \dfrac{{\left| {{{\vec u}_{\left( {AMC} \right)}}.{{\vec u}_{\left( {SBC} \right)}}} \right|}}{{\left| {{{\vec u}_{\left( {AMC} \right)}}} \right|.\left| {.{{\vec u}_{\left( {SBC} \right)}}} \right|}} = \sqrt 5 $
Đáp án cần chọn là: d
Toán Lớp 12
