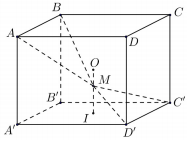
Cho hình lập phương \(ABCD.A'B'C'D'\) có tâm \(O.\) Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và \(M\) là điểm thuộc đoạn thẳng \(OI\) sao cho \(MO = \dfrac{1}{2}MI\) (tham khảo hình vẽ). Khi đó sin của góc tạo bởi mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\) bằng:
Phương pháp giải
Sử dụng phương pháp tọa độ trong không gian để làm bài toán.
Lời giải của Tự Học 365
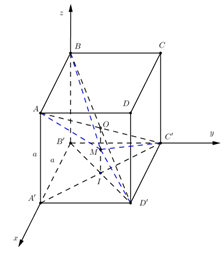
Gọi hình lập phương có cạnh là \(a.\)
Xét hệ trục tọa độ như hình vẽ ta có:
\(\begin{array}{l}B'\left( {0;\;0;\;0} \right),\;\;A'\left( {a;\;0;\;0} \right),\;C'\left( {0;\;a;\;0} \right),\;D'\left( {a;\;a;\;0} \right),\\A\left( {a;\;0;\;a} \right),\;I\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;0} \right),\;B\left( {0;\;0;\;a} \right),\;O\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;\dfrac{a}{2}} \right).\\ \Rightarrow \overrightarrow {OI} = \left( {0;\;0;\;\dfrac{a}{2}} \right) \Rightarrow \overrightarrow {OM} = \dfrac{2}{3}\overrightarrow {OI} = \left( {0;\;0;\;\dfrac{a}{6}} \right).\\ \Rightarrow \left\{ \begin{array}{l}{x_M} - {x_O} = 0\\{y_M} - {y_O} = 0\\{z_M} - {z_O} = \dfrac{a}{6}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{a}{2}\\{y_M} = \dfrac{a}{2}\\{z_M} = \dfrac{{2a}}{3}\end{array} \right. \Rightarrow M\left( {\dfrac{a}{2};\;\dfrac{a}{2};\;\dfrac{{2a}}{3}} \right).\end{array}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {MA} = \left( {\dfrac{a}{2};\; - \dfrac{a}{2};\;\dfrac{a}{3}} \right),\;\overrightarrow {MB} = \left( { - \dfrac{a}{2};\; - \dfrac{a}{2};\;\dfrac{a}{3}} \right),\;\overrightarrow {MC'} = \left( { - \dfrac{a}{2};\;\dfrac{a}{2}; - \dfrac{{2a}}{3}} \right),\;\overrightarrow {MD'} = \left( {\dfrac{a}{2};\;\dfrac{a}{2}; - \dfrac{{2a}}{3}} \right).\\ \Rightarrow {\overrightarrow n _{\left( {MAB} \right)}} = \left[ {\overrightarrow {MA} ,\;\overrightarrow {MB} } \right] = \left( {0; - \dfrac{{{a^2}}}{3}; - \dfrac{{{a^2}}}{2}} \right) = - {a^2}\left( {0;\;\dfrac{1}{3};\;\dfrac{1}{2}} \right).\\{\overrightarrow n _{\left( {MC'D'} \right)}} = \left[ {\overrightarrow {MC'} ,\;\overrightarrow {MD'} } \right] = \left( {0; - \dfrac{{2{a^2}}}{3}; - \dfrac{{{a^2}}}{2}} \right) = - {a^2}\left( {0;\;\dfrac{2}{3};\;\dfrac{1}{2}} \right).\end{array}\)
Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {M'C'D'} \right).\)
$\begin{array}{l} \Rightarrow \cos \alpha = \dfrac{{\left| {{{\overrightarrow n }_{\left( {MAB} \right)}}.{{\overrightarrow n }_{\left( {MC'D'} \right)}}} \right|}}{{\left| {{{\overrightarrow n }_{\left( {MAB} \right)}}} \right|.\left| {{{\overrightarrow n }_{\left( {MC'D'} \right)}}} \right|}} = \dfrac{{\left| {\dfrac{1}{3}.\dfrac{2}{3} + \dfrac{1}{2}.\dfrac{1}{2}} \right|}}{{\sqrt {\dfrac{1}{9} + \dfrac{1}{4}} .\sqrt {\dfrac{4}{9} + \dfrac{1}{4}} }} = \dfrac{{17\sqrt {13} }}{{65}}.\\ \Rightarrow sin\alpha = \sqrt {1 - {{\cos }^2}\alpha } = \dfrac{{6\sqrt {13} }}{{65}}.\end{array}$
Đáp án cần chọn là: d
Toán Lớp 12
