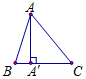
Tam giác $ABC$ là tam giác nhọn có $AA'$ là đường cao.
Khi đó véctơ $\overrightarrow u = \left( {\tan B} \right)\overrightarrow {A'B} + \left( {\tan C} \right)\overrightarrow {A'C} $ là
Phương pháp giải
Viết lại véc tơ \(\overrightarrow u \) sử dụng các công thức \(\tan B = \dfrac{{AA'}}{{BA'}}, \tan C = \dfrac{{AA'}}{{CA'}}\)
Lời giải của Tự Học 365
$\overrightarrow u = \left( {\tan B} \right)\overrightarrow {A'B} + \left( {\tan C} \right) \overrightarrow {A'C} $ $ \Leftrightarrow \overrightarrow u = \dfrac{{AA'}}{{BA'}}\overrightarrow {A'B} + \dfrac{{AA'}}{{CA'}}\overrightarrow {A'C} $.
Ta thấy hai vecto $\dfrac{{AA'}}{{BA'}}\overrightarrow {A'B} $ và $\dfrac{{AA'}}{{CA'}}\overrightarrow {A'C} $ ngược hướng và độ dài mỗi vecto bằng $AA'$ nên chúng là hai vecto đối nhau.
Vậy $\overrightarrow u = \overrightarrow 0 $.
Đáp án cần chọn là: b
Toán Lớp 12
