Lời giải của Tự Học 365

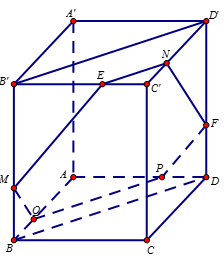
Ta có $\dfrac{{BM}}{{C'N}} = \dfrac{{MB'}}{{ND'}} = \dfrac{{BB'}}{{C'D'}} = 1$, do đó theo định lý ta-let trong không gian thì  $BC'$, $MN$, $B'D'$ lần lượt cùng song song với một mặt phẳng. Mà $B'D'{\rm{//}}\left( {BC'D} \right)$ và $BC' \subset \left( {BC'D} \right)$ nên ta có $MN{\rm{//}}\left( {BC'D} \right)$. Chứng minh tương tự ta có $NP{\rm{//}}\left( {BC'D} \right)$. Do đó $\left( {MNP} \right){\rm{//}}\left( {BC'D} \right)$.

Qua $P$, kẻ $PQ{\rm{//}}BD,Q \in AB$. Qua  $N$, kẻ $NF{\rm{//C'}}D,F \in D'D$.

Qua $M$, kẻ $ME{\rm{//BC'}},E \in B'C'$.

Khi đó ta có thiết diện tạo bởi mặt phẳng $\left( {MNP} \right)$ với hình lập phương là lục giác $MENFPQ$.

Dễ thấy $EN = PF = MQ = \dfrac{{a\sqrt 2 }}{3}$, $NF = PQ = ME = \dfrac{{2a\sqrt 2 }}{3}$ và tam giác  $BC'D$ là tam giác đều vì $BC' = BD = DC' = a\sqrt 2 $. Do đó $\widehat {ENF} = \widehat {NFP} = \widehat {FPQ} = \widehat {PQM} = \widehat {QME} = \widehat {MEN} = 60^\circ $

Suy ra: $E{F^2} = E{N^2} + N{F^2} - 2.EN.NF.\cos 60^\circ  = \dfrac{2}{3}{a^2}$$ \Rightarrow EF = \dfrac{{a\sqrt 6 }}{3}$.

Tương tự thì $FQ = QE = \dfrac{{a\sqrt 6 }}{3}$.

Ta có ${S_{MENFPQ}} = 3.{S_{ENF}} + {S_{EFQ}}$$ = 3.\dfrac{1}{2}.\dfrac{{2a\sqrt 2 }}{3}.\dfrac{{a\sqrt 2 }}{3}.\dfrac{{\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{4}.\dfrac{{2{a^2}}}{3}$$ = \dfrac{{5\sqrt 3 }}{{18}}{a^2}$.

Đáp án cần chọn là: d