Lời giải của Tự Học 365

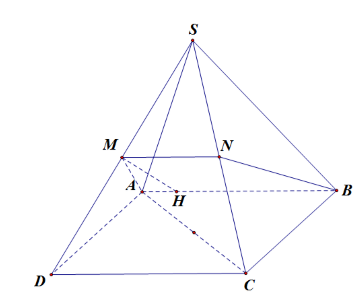
Gọi \(\Delta \) là giao tuyến của mặt phẳng \(\left( {ABM} \right)\) với mặt phẳng \(\left( {SDC} \right)\).

Ta có \(AB\) song song với \(\left( {SDC} \right)\) nên suy ra \(AB\) song song với \(\Delta \).

Gọi \(N\) là trung điểm \(SC\), ta có \(N \in \Delta \).

Do đó thiết diện là hình thang cân \(ABNM\).

Kẻ \(MH \bot AB\) tại \(H\), \(H \in AB\). Do \(AB = CD\) và \(MN < CD\) nên \(H\) thuộc đoạn \(AB\).

Áp dụng công thức độ dài đường trung tuyến, ta có

\(AM = \sqrt {\dfrac{{{a^2} + 2{a^2}}}{2} - \dfrac{{2{a^2}}}{4}}  = a\).

Mặt khác \(AH = \dfrac{{AB - MN}}{2} = \dfrac{{a - \dfrac{a}{2}}}{2} = \dfrac{a}{4}\) nên \(MH = \sqrt {A{M^2} - A{H^2}}  = \dfrac{{a\sqrt {15} }}{4}\).

Suy ra ${S_{ABNM}} = \dfrac{{MH.\left( {MN + AB} \right)}}{2} = \dfrac{{3\sqrt {15} {a^2}}}{{16}}$.

Đáp án cần chọn là: a