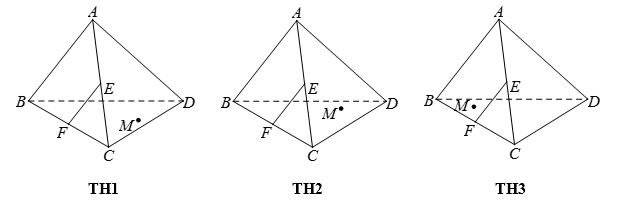
Cho tứ diện \(ABCD\). Gọi \(E\), \(F\) lần lượt là trung điểm của các cạnh \(AC\) và \(BC\). Trên mặt phẳng \(\left( {BCD} \right)\) lấy một điểm \(M\) tùy ý (điểm \(M\) có đánh dấu tròn như hình vẽ). Nêu đầy đủ các trường hợp (TH) để thiết diện tạo bởi mặt phẳng \(\left( {MEF} \right)\) với tứ diện \(ABCD\) là một tứ giác.
Phương pháp giải
Dựng thiết diện theo từng vị trí của \(M\) trong đề, từ đó kết luận trường hợp nào cho ta thiết diện là một tứ giác.
Lời giải của Tự Học 365
Hình ở TH1: Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(CD\) tại \(H\). Thiết diện là tam giác \(EFH\).
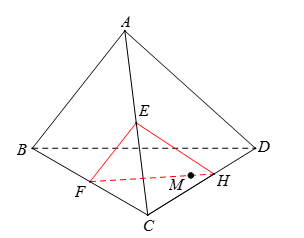
Hình ở TH2:
Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(BD\) tại \(I\), cắt \(CD\) tại \(H\).
Trong \(\left( {ACD} \right)\): Kẻ \(HE\) cắt \(AD\) tại \(K\).
Thiết diện là tứ giác \(EFIK\).
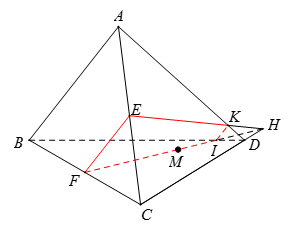
Hình ở TH3:
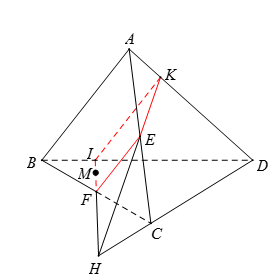
Trong \(\left( {BCD} \right)\): Kẻ \(FM\) cắt \(BD\) tại \(I\), cắt \(CD\) tại \(H\).
Trong \(\left( {ACD} \right)\): Kẻ \(HE\) cắt \(AD\) tại \(K\).
Thiết diện là tứ giác \(EFIK\).
Đáp án cần chọn là: c
Toán Lớp 12
