Lời giải của Tự Học 365

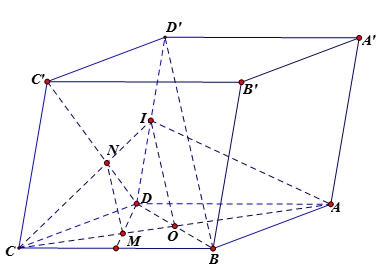
Ta có: \(M\)là điểm trên cạnh \(AC\) sao cho \(AC = 3MC\). Nên \(M\) là trọng tâm của tam giác \(BCD\).

Gọi \(O\) và \(I\) lần lượt là trung điểm của \(AC\) và \(DD'\). Khi đó ta có: \(BD'\;{\rm{//}}\;\left( {IAC} \right)\).

Trong \(\left( {CDD'C'} \right)\), gọi \(N' = CI \cap C'D\). Suy ra \(N'\) là trọng tâm tam giác \(CDD'\).

Do đó: \(\dfrac{{CM}}{{CO}} = \dfrac{2}{3} = \dfrac{{CN'}}{{CI}}\) \( \Rightarrow MN'\;{\rm{//}}\;OI\), mà \(OI\;{\rm{//}}\;BD'\) nên \(MN'\;{\rm{//}}\;BD'\).

Vậy \(N' \equiv N\) và \(x = \dfrac{2}{3}\).

Đáp án cần chọn là: a