Lời giải của Tự Học 365

Vẽ $AH \bot BC$ tại $H,D$ đối xứng với $A$ qua $H$

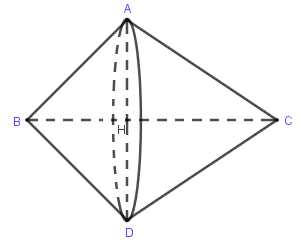
Thể tích khối tròn xoay thu được khi quay $\Delta ABC$ quanh cạnh $BC$ bằng tổng thể tích hai khối nón có chung đường tròn đáy bán kính $AH$. Ta có:

$\dfrac{{3136\pi }}{5} = {V_a} = \dfrac{1}{3}\pi A{H^2}.BH + \dfrac{1}{3}\pi A{H^2}.CH$$ = \dfrac{1}{3}\pi A{H^2}.BC = \dfrac{1}{3}\pi .a.h_a^2$

\( \Rightarrow a{V_a} = \dfrac{1}{3}\pi {a^2}h_a^2 = \dfrac{1}{3}\pi {\left( {2S} \right)^2} = \dfrac{{4\pi }}{3}{S^2}\) với \(S = {S_{ABC}}\).

Tương tự ta có

$\dfrac{{9408\pi }}{{13}} = {V_b} = \dfrac{1}{3}\pi .b.h_b^2 \Rightarrow b{V_b} = \dfrac{{4\pi }}{3}{S^2}$

$672\pi  = {V_c} = \dfrac{1}{3}\pi .c.h_c^2 \Rightarrow c{V_c} = \dfrac{{4\pi }}{3}{S^2}$

$ \Rightarrow a.{V_a} = b.{V_b} = c.{V_c} = \dfrac{{4\pi }}{3}{S^2}\;\left( * \right)$

$ \Rightarrow a:b:c = \dfrac{1}{{{V_a}}}:\dfrac{1}{{{V_b}}}:\dfrac{1}{{{V_c}}} = 15:13:14$

Đặt $a = 15k;b = 13k;c = 14k$. Theo công thức Hêrông, ta có

${S_{ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}  = \sqrt {7056{k^2}}  = 84k$ với $p = \dfrac{{a + b + c}}{2} = 21k$

Từ (*) suy ra $\dfrac{{3{V_a}}}{\pi } = \dfrac{{{{\left( {2{S_{ABC}}} \right)}^2}}}{a} \Rightarrow \dfrac{{9408}}{5} = \dfrac{{{{\left( {168k} \right)}^2}}}{{15k}} \Rightarrow k = 1 \Rightarrow {S_{ABC}} = 84$

Đáp án cần chọn là: a