Lời giải của Tự Học 365

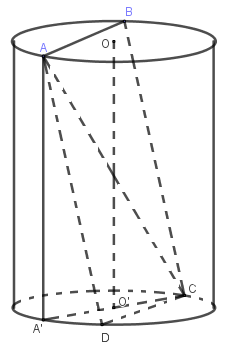
Vì $AB = CD;\,\,AB$//$CD$$ \Rightarrow \,\,ABCD$ là hình chữ nhật $ \Rightarrow \,\,AD = 10\,\,cm.$

Xét hình chữ nhật \(ABCD\) có \(AD\) không song song và không vuông góc với trục \(OO'\) của hình trụ.

Dựng đường sinh $AA'$, ta có \(\left\{ \begin{array}{l}CD \bot AA'\\CD \bot AD\end{array} \right. \Rightarrow CD \bot \left( {AA'D} \right) \Rightarrow CD \bot A'D\)

Suy ra \(A'C\) là đường kính đáy nên \(A'C = 2R\)

Xét tam giác vuông \(AA'C,\) có \(A'C = \sqrt {A{C^2} - A{{A'}^2}}  = \sqrt {{{\left( {2\sqrt {34} } \right)}^2} - {{\left( {6\sqrt 2 } \right)}^2}}  = 8.\)

Suy ra độ dài bán kính đáy của hình trụ là \(2R = 8 \Leftrightarrow R = 4\,\,cm.\)

Đáp án cần chọn là: d