Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có trực tâm \(O\). Gọi \(M\) là trung điểm của \(BC\); \(N\), \(P\) lần lượt là chân đường cao kẻ từ \(B\) và \(C\). Đường tròn đi qua ba điểm \(M\), \(N\), \(P\) có phương trình là \(\left( T \right):{\left( {x - 1} \right)^2} + {\left( {y + \dfrac{1}{2}} \right)^2} = \dfrac{{25}}{4}\). Phương trình đường tròn ngoại tiếp tam giác \(ABC\) là:
Phương pháp giải
Ta có \(M\) là trung điểm của \(BC\); \(N\), \(P\) lần lượt là chân đường cao kẻ từ \(B\) và \(C\). Đường tròn đi qua ba điểm \(M\), \(N\), \(P\) là đường tròn Euler. Do đó đường tròn ngoại tiếp tam giác \(ABC\) chính là ảnh của đường tròn Euler qua phép vị tự tâm là \(O\), tỷ số \(k = 2\).
Lời giải của Tự Học 365
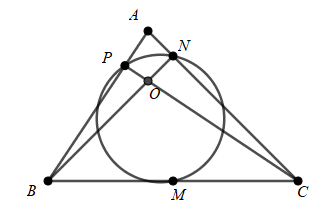
Gọi \(I\) và \(I'\) lần lượt là tâm đường tròn ngoại tiếp tam giác \(MNP\) và tam giác \(ABC\).
Gọi \(R\) và \(R'\) lần lượt là bán kính đường tròn ngoại tiếp tam giác \(MNP\) và tam giác \(ABC\).
Ta có \(I\left( {1; - \dfrac{1}{2}} \right)\) và do đó \(\overrightarrow {OI'} = 2\overrightarrow {OI} \Rightarrow I'\left( {2;\; - 1} \right)\).
Mặt khác \(R = \dfrac{5}{2} \Rightarrow R' = 5\).
Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là: \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 25\).
Đáp án cần chọn là: d
Toán Lớp 12
