Lời giải của Tự Học 365

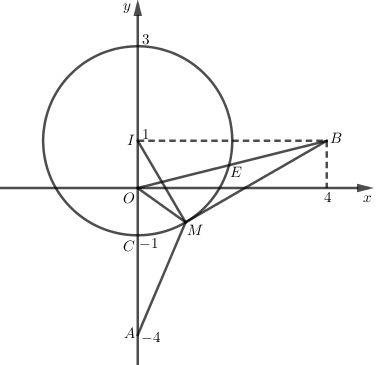
Trên mặt phẳng tọa độ Oxy, gọi \(A\left( 0;-3 \right)\) là điểm biểu diễn số phức \({{z}_{1}};\,\,B\left( 4;1 \right)\) là điểm biểu diễn số phức \({{z}_{2}};\,\,I\left( 0;1 \right)\) là điểm biểu diễn số phức i và M là điểm biểu diễn cho số phức z.

Theo đề bài ta có \(\left| z-i \right|=2\Rightarrow MI=2\Rightarrow \) M thuộc đường tròn tâm I bán kính R = 2.

\(T=\left| z-{{z}_{1}} \right|+2\left| z-{{z}_{2}} \right|=MA+2MB\).

Ta có IM = 2, IO = 1, IA = 4 \(\Rightarrow I{{M}^{2}}=IA.IO\Leftrightarrow \dfrac{IM}{IA}=\dfrac{IO}{IM}\).

Do đó tam giác IMO đồng dạng với tam giác IAM \(\Rightarrow \dfrac{IM}{IA}=\dfrac{OM}{AM}=\dfrac{1}{2}\Rightarrow MA=2MO\)

\(\Rightarrow T=MA+2MB=2MO+2MB=2\left( MO+MB \right)\ge 2OB\).

Dấu bằng xảy ra khi và chỉ khi M là giao điểm của OB và (I) \(\Leftrightarrow M\equiv E\).

\(O\left( 0;0 \right);\,\,B\left( 4;1 \right)\Rightarrow \) Phương trình OB là \(y=\dfrac{1}{4}x\,\,\left( d \right);\,\,E\in d\Rightarrow E\left( 4m;m \right)\,\,\,\left( m>0 \right)\).

Vì \(E\in \left( I \right)\Rightarrow IE=2\Rightarrow {{\left( 4m \right)}^{2}}+{{\left( m-1 \right)}^{2}}=4\Leftrightarrow 17{{m}^{2}}-2m-3=0\Leftrightarrow m=\dfrac{1+2\sqrt{13}}{17}\,\,\left( m>0 \right)\)

Ta có \(\left\{ \begin{align}  a=4m \\  b=m \\ \end{align} \right.\Rightarrow a-b=3m=\dfrac{3+6\sqrt{13}}{17}\).

Đáp án cần chọn là: c