Lời giải của Tự Học 365

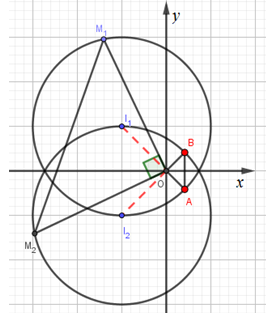
$\left| {{z_1} + 1 - i} \right| = 2 \to $ Tập hợp các điểm biểu diễn ${z_1}$ là đường tròn tâm ${I_1}( - 1;1)$, bán kính $R = 2$

${z_2} = i{z_1}$$ \Rightarrow \left| {\dfrac{{{z_2}}}{i} + 1 - i} \right| = 2 \Leftrightarrow \left| {\dfrac{{{z_2} + i + 1}}{i}} \right| = 2 \Leftrightarrow \dfrac{{\left| {{z_2} + i + 1} \right|}}{{\left| i \right|}} = 2 \Leftrightarrow \left| {{z_2} + i + 1} \right| = 2 \to $ Tập hợp các điểm biểu diễn ${z_2}$ là đường tròn tâm ${I_2}( - 1; - 1)$, bán kính $R = 2$.

Gọi ${M_1},\,\,{M_2}$ lần lượt là điểm biểu diễn ${z_1},\,\,{z_2}$$ \Rightarrow {M_1} \in \left( {{I_1};R} \right),\,\,\,{M_2} \in \left( {{I_2};R} \right)$

và $\left| {{z_1} - {z_2}} \right| = {M_1}{M_2}$.

Mặt khác ${z_2} = i{z_1}$ nên giả sử ${z_1} = a + bi \Rightarrow {z_2} =  - b + ai \Rightarrow {M_1}\left( {a;b} \right),\,\,{M_2}\left( { - b;a} \right) \Rightarrow \overrightarrow {O{M_1}} .\overrightarrow {O{M_2}}  = 0 \Rightarrow O{M_1} \bot O{M_2}$

Dễ thấy, tam giác $O{M_1}{M_2}$ là tam giác vuông cân tại O. Khi đó, để ${M_1}{M_2}$ngắn nhất thì $O{M_1} = O{M_2}$ ngắn nhất

$ \Rightarrow {M_1},\,\,{M_2}$ lần lượt trùng với A, B; là giao điểm của $O{I_1},\,\,O{I_2}$ và $\left( {{I_1};R} \right);\,\left( {{I_2};R} \right)\,$, (A nằm khác phía ${I_1}$ so với O,  B nằm khác phía ${I_2}$ so với O).

+) Tìm tọa độ điểm A:

$A\left( {a;b} \right) \in \left( {{I_1};R} \right) \Rightarrow {\left( {a + 1} \right)^2} + {(b - 1)^2} = 4$

$\begin{array}{l}A \in {I_1}O \Rightarrow b =  - a\\ \Rightarrow {\left( {a + 1} \right)^2} + {\left( { - a - 1} \right)^2} = 4 \Leftrightarrow {\left( {a + 1} \right)^2} = 2 \Leftrightarrow a =  - 1 \pm \sqrt 2  \Rightarrow a =  - 1 + \sqrt 2 \\ \Rightarrow A\left( { - 1 + \sqrt 2 ;1 - \sqrt 2 } \right)\\ \Rightarrow OA = \sqrt {{{\left( { - 1 + \sqrt 2 } \right)}^2} + {{\left( {1 - \sqrt 2 } \right)}^2}}  = \sqrt 2 \left( {\sqrt 2  - 1} \right) = 2 - \sqrt 2 \\ \Rightarrow AB = \sqrt 2 .OA = 2\sqrt 2  - 2\\ \Rightarrow m = 2\sqrt 2  - 2.\end{array}$

Đáp án cần chọn là: c