Lời giải của Tự Học 365

Theo bài ra ta có số tiền gia đình cần trả là $160.x + 110.y$ với $\,x$,$y$ thỏa mãn: $\left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\end{array} \right.$.

Số đơn vị protein gia đình có là $0,8.x + 0,6.y \ge 0,9$$\Leftrightarrow 8x + 6y \ge 9$$\left( {{d_1}} \right)$.

Số đơn vị lipit gia đình có là$0,2.x + 0,4.y \ge 0,4 \Leftrightarrow \,x + 2y \ge 2$ $\left( {{d_2}} \right)$.

Bài toán trở thành: Tìm $x,y$ thỏa mãn hệ bất phương trình $\left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\8x + 6y \ge 9\\x + 2y \ge 2\end{array} \right.$ sao cho $T = 160.x + 110.y$ nhỏ nhất.

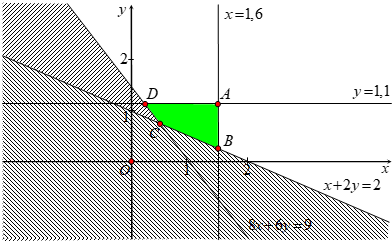
Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm $A\left( {1,6;\,1,1} \right)$; $B\left( {1,6;\,0,2} \right)$; $C\left( {0,6;\,0,7} \right)$; $D\left( {0,3;\,1,1} \right)$.

Nhận xét: $T\left( A \right) = 377$ nghìn, $T\left( B \right) = 278$ nghìn, $T\left( C \right) = 173$ nghìn, $T\left( D \right) = 169$ nghìn.

Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì $x = 0,6$ và $y = 0,7$.

Đáp án cần chọn là: c