Cho bất phương trình \({x^2} - 6x + \sqrt { - {x^2} + 6x - 8} + m - 1 \ge 0\). Xác định \(m\) để bất phương trình nghiệm đúng với \(\forall x \in \left[ {2; 4} \right]\).
Phương pháp giải
- Biến đổi bất phương trình về dạng \(m \ge f\left( t \right)\) với \(t = \sqrt { - {x^2} + 6x - 8} \)
- Sử dụng phương pháp hàm số xét hàm \(f\left( t \right)\) với điều kiện \(t\) tìm được theo điều kiện của \(x\)
- Bất phương trình \(m \ge f\left( t \right)\) với \(\forall t \in D\) nếu \(m \ge \mathop {\max }\limits_D f\left( t \right)\)
Lời giải của Tự Học 365
Điều kiện \( - {x^2} + 6x - 8 \ge 0\)\( \Leftrightarrow x \in \left[ {2; 4} \right]\).
Đặt \(t = \sqrt { - {x^2} + 6x - 8} \) \(\left( {0 \le t \le 1} \right)\)suy ra \({x^2} - 6x = - 8 - {t^2}\).
Ta có bất phương trình \( - 8 - {t^2} + t + m - 1 \ge 0\) \( \Leftrightarrow m \ge {t^2} - t + 9\) \((*)\).
Xét \(f\left( t \right) = {t^2} - t + 9\) trên \(\left[ {0; 1} \right]\) ta có bảng biến thiên như sau:
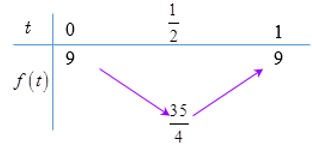
Để bất phương trình đã cho nghiệm đúng \(\forall x \in \left[ {2; 4} \right]\) thì bất phương trình \(\left( * \right)\) nghiệm đúng với mọi \(t \in \left[ {0; 1} \right]\) \( \Leftrightarrow m \ge 9\).
Đáp án cần chọn là: d
Toán Lớp 12
