Lời giải của Tự Học 365

Đặt \(x + \dfrac{1}{x} = t\), \(\left| t \right| \ge 2\) khi đó phương trình trở thành \(2{t^2} - 3t - 5m - 3 = 0\) (*)

Phương trình \(2\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 3\left( {x + \dfrac{1}{x}} \right) - 5m + 1 = 0\) có nghiệm khi và chỉ khi phương trình (*) có nghiệm \(t\) thỏa mãn \(\left| t \right| \ge 2\).

Số nghiệm của phương trình (*) bằng số giao điểm của parabol \(\left( P \right):y = 2{t^2} - 3t - 3\) và đường thẳng \(d:y = 5m\).

Xét parabol \(\left( P \right):y = 2{t^2} - 3t - 3\) ta có bảng biến thiên như sau

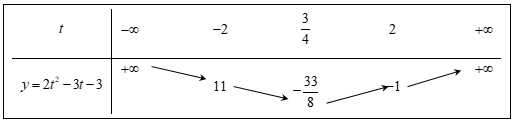
Từ bảng biến thiên ta có phương trình (*) có nghiệm $t \in \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)$ khi và chỉ khi \(5m \ge  - 1\) hoặc $5m\ge 11$

\( \Leftrightarrow m \ge  - \dfrac{1}{5}\) hoặc $m \ge \dfrac{11}{5} $

\( \Leftrightarrow m \ge  - \dfrac{1}{5}\)

Vậy khi \(m \in \left[ { - \dfrac{1}{5}; + \infty } \right)\) thì phương trình có nghiệm \( \Rightarrow \left\{ \begin{array}{l}a = 1\\b = 5\end{array} \right.\) \( \Rightarrow T = 5\).

Đáp án cần chọn là: b