Lời giải của Tự Học 365

Ta có ${x^2} - 2x - 3 - 2m = 0$\( \Leftrightarrow {x^2} - 2x - 3 = 2m\).

Để phương trình đã cho có đúng một nghiệm $x \in \left[ {0;4} \right]$ thì đường thẳng \(y = 2m\) cắt đồ thị hàm số \(y = {x^2} - 2x - 3\) trên \(\left[ {0;4} \right]\) tại một điểm duy nhất.

Lập bảng biến thiên của hàm số trên $[0;4]$

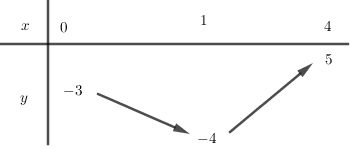
Dựa vào bảng biến thiên ta có:

Để phương trình đã cho có nghiệm duy nhất thuộc $[0;4]$ thì \(\left[ \begin{array}{l}2m =  - 4\\ - 3 < 2m \le 5\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}m =  - 2\\ - \dfrac{3}{2} < m \le \dfrac{5}{2}\end{array} \right.\)

Vậy các giá trị nguyên của \(m\) thỏa mãn là \(m \in \left\{ { - 2; - 1;0;1;2} \right\}\)

Đáp án cần chọn là: a