Lời giải của Tự Học 365

Đặt \(t = \sqrt {x + 2}  + \sqrt {2 - x} \)

Điều kiện \(t = \sqrt {x + 2}  + \sqrt {2 - x}  \ge \sqrt {x + 2 + 2 - x}  = 2 \Rightarrow t \ge 2\)

Lại có \(\sqrt {x + 2}  + \sqrt {2 - x}  \le \sqrt {{1^2} + {1^2}} .\sqrt {x + 2 + 2 - x}  = 2\sqrt 2 \) \( \Rightarrow t \le 2\sqrt 2 \)

Suy ra \(2 \le t \le 2\sqrt 2 \)

Ta có: \({t^2} = 4 + 2\sqrt {4 - {x^2}} \)\( \Rightarrow 2\sqrt {4 - {x^2}}  = {t^2} - 4\)

Phương trình trở thành: \(t + {t^2} - 4 - 2m + 3 = 0\)\( \Leftrightarrow {t^2} + t - 2m - 1 = 0\)\( \Leftrightarrow {t^2} + t - 1 = 2m\,\,\,(*)\)

Xét hàm số \(f\left( t \right) = {t^2} + t - 1\) (parabol có hoành độ đỉnh \(x =  - \dfrac{1}{2} otin \left[ {2;2\sqrt 2 } \right]\)) trên \(\left[ {2;2\sqrt 2 } \right]\), có bảng biến thiên

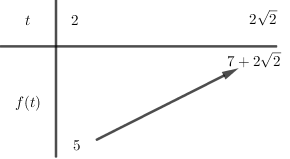
Phương trình $(*)$ có nghiệm thỏa \(2 \le t \le 2\sqrt 2 \) khi \(5 \le 2m \le 7 + 2\sqrt 2 \)\( \Rightarrow \dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\)

\(\dfrac{5}{2} \le m \le \dfrac{{7 + 2\sqrt 2 }}{2}\,\)\( \to \left( {2,5 \le m \le 4,91} \right)\)

Vậy có 2 giá trị \(m\) nguyên dương là \(m = 3\), \(m = 4\).

Đáp án cần chọn là: d