Lời giải của Tự Học 365

Ta có ${2017^{2x + \sqrt {x + 1} }} - {2017^{2 + \sqrt {x + 1} }} + 2018x \le 2018$

$ \Leftrightarrow {2017^{2x + \sqrt {x + 1} }} + 1009\left( {2x + \sqrt {x + 1} } \right) \le {2017^{2 + \sqrt {x + 1} }} + 1009\left( {2 + \sqrt {x + 1} } \right)$$ \Leftrightarrow f\left( {2x + \sqrt {x + 1} } \right) \le f\left( {2 + \sqrt {x + 1} } \right)$

Xét hàm số $f\left( u \right) = {2017^u} + 1009u$

Ta có $f'\left( t \right) = {2017^u}\ln 2017 + 1009 > 0,\forall u$$ \Rightarrow f\left( u \right)$ đồng biến.

Nên $2x + \sqrt {x + 1}  \le 2 + \sqrt {x + 1}  \Leftrightarrow  - 1 \le x \le 1$

Ta lại có $5{x^2} + 12x + 16 = m\left( {x + 2} \right)\sqrt {{x^2} + 2} $$ \Leftrightarrow 3{\left( {x + 2} \right)^2} + 2\left( {{x^2} + 2} \right) = m\left( {x + 2} \right)\sqrt {{x^2} + 2} $

$ \Rightarrow 3{\left( {\dfrac{{x + 2}}{{\sqrt {{x^2} + 2} }}} \right)^2} + 2 = m.\dfrac{{x + 2}}{{\sqrt {{x^2} + 2} }}$

Xét $t = \dfrac{{x + 2}}{{\sqrt {{x^2} + 2} }} \Rightarrow t'\left( x \right) = \dfrac{{2 - 2x}}{{{{\left( {\sqrt {{x^2} + 2} } \right)}^3}}} \ge 0,\forall x \in \left[ { - 1;1} \right]$

Nên $\dfrac{{\sqrt 3 }}{3} \le t \le \sqrt 3 $

Khi đó phương trình trở thành $3{t^2} + 2 = mt \Leftrightarrow 3t + \dfrac{2}{t} = m$

Xét hàm số $g\left( t \right) = 3t + \dfrac{2}{t}$.

Ta có $g'\left( t \right) = 3 - \dfrac{2}{{{t^2}}} = \dfrac{{3{t^2} - 2}}{{{t^2}}}$.

Cho $g'\left( t \right) = 0 \Rightarrow t = \dfrac{{\sqrt 6 }}{3}$

Bảng biến thiên:

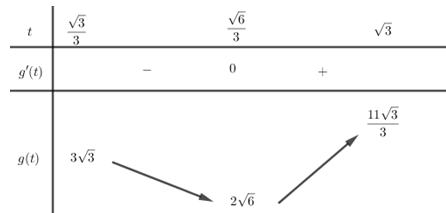
Dựa vào bảng biến thiên suy ra $2\sqrt 6  < m \le 3\sqrt 3 $.

Đáp án cần chọn là: a