Lời giải của Tự Học 365

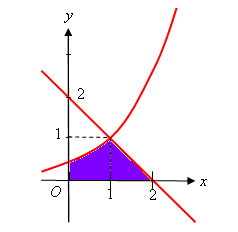
Phương trình hoành độ giao điểm của đường cong \(y = {{\rm{e}}^{x - 1}}\) và đường thẳng \(y = 2 - x\): ${{\rm{e}}^{x - 1}} = 2 - x \Leftrightarrow x = 1$.

(Vì \(y = {{\rm{e}}^{x - 1}}\) là hàm đồng biến và \(y = 2 - x\) là hàm nghịch biến trên tập xác định \(\mathbb{R}\) nên phương trình có tối đa \(1\) nghiệm. Mặt khác $x = 1$ thỏa mãn pt nên đó là nghiệm duy nhất của pt đó).

Đường thẳng \(y = 2 - x\) cắt trục hoành tại điểm có hoành độ \(x = 2\).

\(V = \pi \int\limits_0^1 {{{\left( {{{\rm{e}}^{x - 1}}} \right)}^2}{\rm{d}}x}  + \pi \int\limits_1^2 {{{\left( {2 - x} \right)}^2}{\rm{d}}x} \)\( = \left. \dfrac{1}{2}{\pi {{\rm{e}}^{2x - 2}}} \right|_0^1 + \left. {\pi \left( {\dfrac{{{x^3}}}{3} - 2x + 4} \right)} \right|_1^2 = \dfrac{{\pi \left( {5{{\rm{e}}^2} - 3} \right)}}{{6{{\rm{e}}^2}}}\)

Đáp án cần chọn là: b