Lời giải của Tự Học 365

Gọi phương trình parabol \(\left( P \right):y = a{x^2} + bx + c\). Do tính đối xứng của parabol nên ta có thể chọn hệ trục tọa độ \(Oxy\) sao cho \(\left( P \right)\) có đỉnh $I\left( {0;\dfrac{9}{4}} \right)\in Oy $ và đi qua hai điểm $A\left( { - \dfrac{3}{2};0} \right),B\left( {\dfrac{3}{2};0} \right)$ (như hình vẽ).

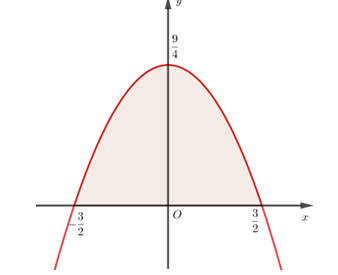
Ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{9}{4} = c,\left( {I \in \left( P \right)} \right)\\\dfrac{9}{4}a - \dfrac{3}{2}b + c = 0\left( {A \in \left( P \right)} \right)\\\dfrac{9}{4}a + \dfrac{3}{2}b + c = 0\left( {B \in \left( P \right)} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}c = \dfrac{9}{4}\\a =  - 1\\b = 0\end{array} \right.\)

Vậy \(\left( P \right):y =  - {x^2} + \dfrac{9}{4}\)

Dựa vào đồ thị, diện tích cửa parabol là:

\(S = \int\limits_{\frac{{ - 3}}{2}}^{\frac{3}{2}} {\left( { - {x^2} + \dfrac{9}{4}} \right){d}x} \)\( = 2\int\limits_0^{\frac{3}{2}} {\left( { - {x^2} + \dfrac{9}{4}} \right){d}x} \)$ = \left. {2\left( {\dfrac{{ - {x^3}}}{3} + \dfrac{9}{4}x} \right)} \right|_0^{\frac{9}{4}}$ \( = \dfrac{9}{2}{{\rm{m}}^2}\)

Số tiền phải trả là: \(\dfrac{9}{2}.1500000 = 6750000\) đồng

Đáp án cần chọn là: d