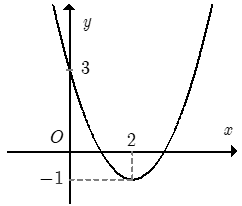
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số $m$ thì phương trình $\left| {f\left( x \right)} \right| - 1 = m$ có đúng \(2\) nghiệm phân biệt.
Phương pháp giải
- Dựng đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) từ đồ thị hàm số \(y = f\left( x \right)\) bằng cách giữ nguyên phần phía trên \(Ox\), lấy đối xứng phần dưới qua \(Ox\) đồng thời xóa phần dưới cũ.
- Tìm \(m\) để phương trình \(\left| {f\left( x \right)} \right| = m + 1\) có đúng hai nghiệm phân biệt, sử dụng mối quan hệ số nghiệm của phương trình với số giao điểm hai đồ thị hàm số.
Lời giải của Tự Học 365
+ Phương trình $ \Leftrightarrow \left| {f\left( x \right)} \right| = m + 1$.
+ Đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có dạng:
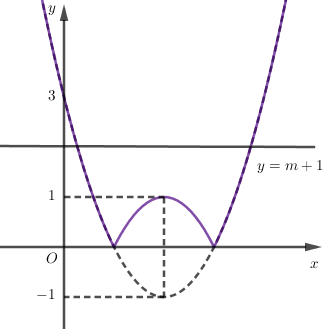
+ Dựa vào đồ thị, để phương trình $\left| {f\left( x \right)} \right| = m + 1$ có hai nghiệm phân biệt thì:
\(\left[ \begin{array}{l}m + 1 > 1\\m + 1 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}m > 0\\m = - 1\end{array} \right.\).
Đáp án cần chọn là: b
Toán Lớp 12
