Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
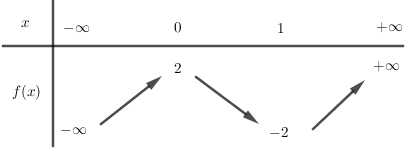
Phương pháp giải
Lập bảng biến thiên của hàm số \(y = \left| {f\left( x \right) - 1} \right|\) với chú ý:
+ Đồ thị hàm số \(y = f\left( x \right) - 1\) có được từ việc tịnh tiến \(y = f\left( x \right)\) xuống dưới \(1\) đơn vị.
+ Đồ thị hàm số \(y = \left| {f\left( x \right)}-1 \right|\) có được từ việc giữ nguyên phần đồ thị \(y = f\left( x \right)-1\) phía trên trục hoành và lấy đối xứng phần dưới qua trục hoành, đồng thời xóa bỏ phần dưới cũ.
Lời giải của Tự Học 365
Dựa vào bảng biến thiên của hàm số \(y = f\left( x \right)\), ta có bảng biến thiên của hàm số \(y = f\left( x \right) - 1\) là:
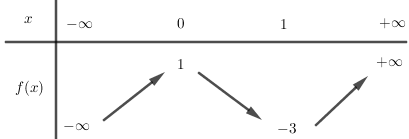
Suy ra bảng biến thiên của hàm số \(y = \left| {f\left( x \right) - 1} \right|\)
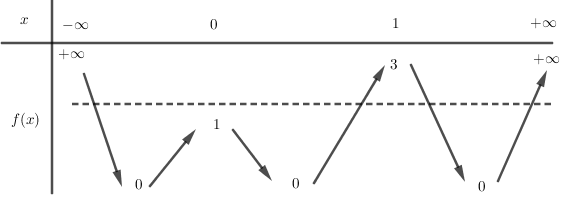
Từ BBT suy ra phương trình \(\left| {f\left( x \right) - 1} \right| = m\) có bốn nghiệm phân biệt khi \(1 < m < 3\).
Vậy \(1 < m < 3\).
Đáp án cần chọn là: b
Toán Lớp 12
