Lời giải của Tự Học 365

Ta có: $y = {x^2} - 6\left| x \right| + 5 = \left\{ \begin{array}{l} {x^2} - 6x + 5\,\,\,khi\,x \ge 0\,\,\left( {{C_1}} \right)\\ {x^2} + 6x + 5\,\,\,khi\,x < 0\,\,\left( {{C_2}} \right)\end{array} \right.$

Đồ thị $\,\left( C \right)$của hàm số \(y = {x^2} - 6\left| x \right| + 5\) gồm hai phần

Phần đồ thị $\left( {{C_1}} \right)$: là phần đồ thị của hàm số \({y_1} = {x^2} - 6x + 5\,\)nằm bên phải trục tung

Phần đồ thị $\,\left( {{C_2}} \right)$: là phần đồ thị của hàm số \({y_2} = {x^2} + 6x + 5\) có được bằng cách lấy đối xứng phần đồ thị $\left( {{C_1}} \right)$ qua trục tung

Ta có đồ thị $\,\left( C \right)$ như hình vẽ

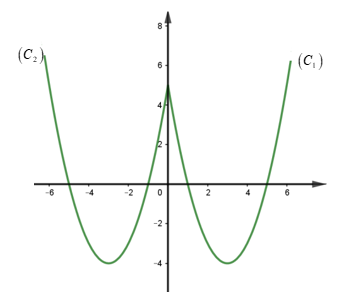
Vậy: đồ thị $\,\left( C \right)$ có trục đối xứng có phương trình \(x = 0\) và nó không có tâm đối xứng.

Đáp án cần chọn là: d