Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau.
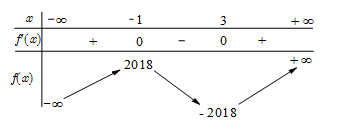
Đồ thị hàm số \(y = \left| {f\left( {x - 2017} \right) + 2018} \right|\) có bao nhiêu điểm cực trị?
Phương pháp giải
- Lập bảng biến thiên của hàm số \(y = f\left( {x - 2017} \right) + 2018\)
- Từ đó suy ra bảng biến thiên của hàm số \(y = \left| {f\left( {x - 2017} \right) + 2018} \right|\) và kết luận đáp án đúng.
Lời giải của Tự Học 365
Do hàm số \(g\left( x \right) = f\left( {x - 2017} \right) + 2018\) thu được bằng cách tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải một đoạn có độ dài bằng $2017$ đơn vị và tịnh tiến lên trên một đoạn có độ dài bằng $2018$ đơn vị nên ta có bảng biến thiên của hàm số \(y = g\left( x \right)\) như sau
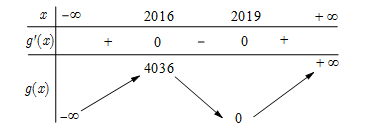
Do đó ta có bảng biến thiên của hàm số \(y = \left| {g\left( x \right)} \right|\) là:
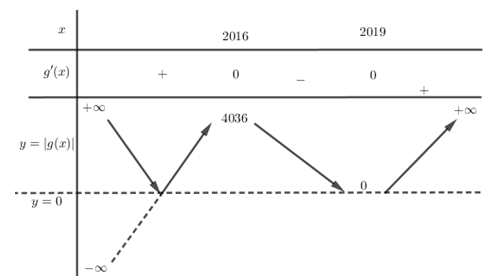
Vậy đồ thị hàm số \(y = \left| {f\left( {x - 2017} \right) + 2018} \right|\) có $3$ cực trị.
Đáp án cần chọn là: b
Toán Lớp 12
